Hệ thống cáp treo núi Bà Đen tỉnh Tây Ninh gồm hai tuyến Vân Sơn và Chùa Hang có tổng cộng 191 cabin, mỗi cabin có sức chứa 10 người. Nếu tất cả các cabin của hai tuyến đều chứa đủ số người theo qui định thì số người ở tuyến Vân Sơn nhiều hơn số người ở tuyến Chùa Hang là 350 người. Tính số cabin của mỗi tuyến.
Hệ thống cáp treo núi Bà Đen tỉnh Tây Ninh gồm hai tuyến Vân Sơn và Chùa Hang có tổng cộng 191 cabin, mỗi cabin có sức chứa 10 người. Nếu tất cả các cabin của hai tuyến đều chứa đủ số người theo qui định thì số người ở tuyến Vân Sơn nhiều hơn số người ở tuyến Chùa Hang là 350 người. Tính số cabin của mỗi tuyến.
Quảng cáo
Trả lời:
Gọi số cabin của tuyến Vân Sơn là \(x\) (cabin) \(\left( {x \in {\mathbb{Z}^ + }, x < 191} \right)\)
Gọi số cabin của tuyến Chùa Hang là \(y\) (cabin) \(\left( {y \in {\mathbb{Z}^ + }, y < 191} \right)\)
Hai tuyến Vân Sơn và Chùa Hang có tổng cộng 191 cabin nên:
\(x + y = 191\)
Vì số người ở tuyến Vân Sơn nhiều hơn số người ở tuyến Chùa Hang là 350 người (nếu mỗi cabin chứa đủ 10 người) nên:
\(10x - 10y = 350\) hay \(x - y = 35\)
Ta có hệ phương trình
\(\left\{ {\begin{array}{*{20}{c}}{x + y = 191}\\{x - y = 35}\end{array}} \right.\) \( \Leftrightarrow \)\(\left\{ {\begin{array}{*{20}{c}}{x + y = 191}\\{2x = 226}\end{array}} \right.\) \( \Leftrightarrow \)\(\left\{ {\begin{array}{*{20}{c}}{x = 113 (nha\"a n)}\\{y = 78 (nha\"a n)}\end{array}} \right.\)
Vậy tuyến Vân Sơn có 113 cabin tuyến Chùa Hang có 78 cabin.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
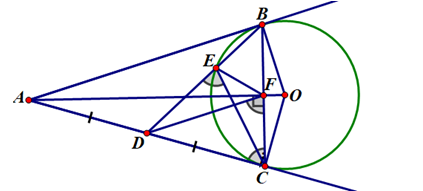
Ta có \(OA \bot BC\) tại F (vì \(OB = OC\) và \(AB = AC\))
\(\Delta ACF\) vuông ở F, trung tuyến FD
\( \Rightarrow \)\(DF = DC = \frac{1}{2}AC\) \( \Rightarrow \)\(\widehat {DFC} = \widehat {DCF}\) (1)
(vì \(\widehat {BDC}\) chung, )
\( \Rightarrow \)\(\widehat {DEC} = \widehat {DCB}\) hay \(\widehat {DEC} = \widehat {DCF}\) (2)
(1), (2) suy ra \(\widehat {DEC} = \widehat {DFC}\)
\( \Rightarrow \)Tứ giác CDEF nội tiếp được.
Hay bốn điểm C, D, E, F cùng thuộc một đường tròn.
Cách 2:
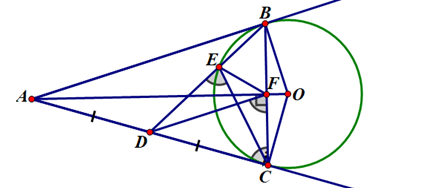
Ta có OA là trung trực của đoạn BC (vì \(OB = OC\) và \(AB = AC\))
\(OA \bot BC\) tại F và \(FB = FC\)
DF là đường trung bình của \(\Delta ABC\) \( \Rightarrow \)\(DF\parallel AB\)
\( \Rightarrow \)\(\widehat {EDF} = \widehat {ABD}\) (so le trong, \(DF\parallel AB\)) (1)
\( \Rightarrow \) (2)
(1), (2) suy ra \(\widehat {EDF} = \widehat {ECF}\) \( \Rightarrow \)Tứ giác CDEF nội tiếp được.
Hay bốn điểm C, D, E, F cùng thuộc một đường tròn.
Lời giải
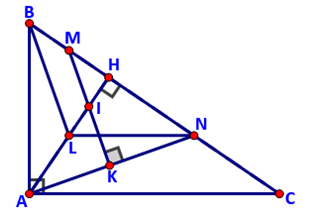
Lấy điểm L đối xứng với H qua I.
\(MI\parallel BL\) (MI là đường trung bình \(\Delta HBL\))
\(MI \bot AN\) (vì \(MK \bot AN\))
Do đó \(BL \bot AN\)
\(\Delta ABN\) có L là trực tâm (giao điểm 2 đường cao AH và BL)
Suy ra \(NL \bot AB\)
\(NL \bot AB\), \(AC \bot AB\) suy ra \(NL\parallel AC\)
\(\Delta HAC\) có \(NH = NC\)và \(NL\parallel AC\) nên \(AL = LH\)
Từ đó \(AL = LH = 2.IH\), suy ra \(AH = 4.IH\) và \(AI = 3.IH\).
Do đó \(\frac{{AH}}{{AI}} = \frac{4}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.