Cho đường tròn (O) và điểm A nằm ngoài (O). Từ A vẽ các tiếp tuyến AB, AC với (O) (B và C là các tiếp điểm). Gọi D là trung điểm của đoạn thẳng AC, BD cắt (O) tại E (khác B) và BC cắt OA tại F. Chứng minh bốn điểm C, D, E, F cùng thuộc một đường tròn.
Cho đường tròn (O) và điểm A nằm ngoài (O). Từ A vẽ các tiếp tuyến AB, AC với (O) (B và C là các tiếp điểm). Gọi D là trung điểm của đoạn thẳng AC, BD cắt (O) tại E (khác B) và BC cắt OA tại F. Chứng minh bốn điểm C, D, E, F cùng thuộc một đường tròn.
Quảng cáo
Trả lời:
Giải bởi Vietjack
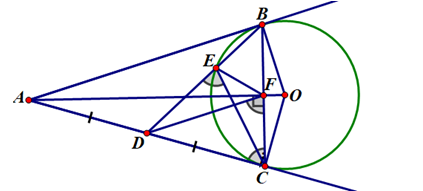
Ta có \(OA \bot BC\) tại F (vì \(OB = OC\) và \(AB = AC\))
\(\Delta ACF\) vuông ở F, trung tuyến FD
\( \Rightarrow \)\(DF = DC = \frac{1}{2}AC\) \( \Rightarrow \)\(\widehat {DFC} = \widehat {DCF}\) (1)
(vì \(\widehat {BDC}\) chung, )
\( \Rightarrow \)\(\widehat {DEC} = \widehat {DCB}\) hay \(\widehat {DEC} = \widehat {DCF}\) (2)
(1), (2) suy ra \(\widehat {DEC} = \widehat {DFC}\)
\( \Rightarrow \)Tứ giác CDEF nội tiếp được.
Hay bốn điểm C, D, E, F cùng thuộc một đường tròn.
Cách 2:
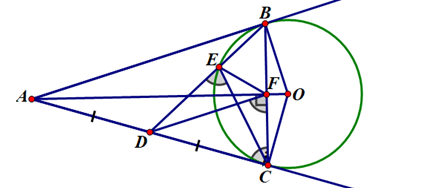
Ta có OA là trung trực của đoạn BC (vì \(OB = OC\) và \(AB = AC\))
\(OA \bot BC\) tại F và \(FB = FC\)
DF là đường trung bình của \(\Delta ABC\) \( \Rightarrow \)\(DF\parallel AB\)
\( \Rightarrow \)\(\widehat {EDF} = \widehat {ABD}\) (so le trong, \(DF\parallel AB\)) (1)
\( \Rightarrow \) (2)
(1), (2) suy ra \(\widehat {EDF} = \widehat {ECF}\) \( \Rightarrow \)Tứ giác CDEF nội tiếp được.
Hay bốn điểm C, D, E, F cùng thuộc một đường tròn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
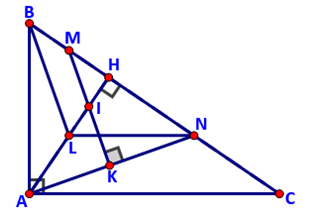
Lấy điểm L đối xứng với H qua I.
\(MI\parallel BL\) (MI là đường trung bình \(\Delta HBL\))
\(MI \bot AN\) (vì \(MK \bot AN\))
Do đó \(BL \bot AN\)
\(\Delta ABN\) có L là trực tâm (giao điểm 2 đường cao AH và BL)
Suy ra \(NL \bot AB\)
\(NL \bot AB\), \(AC \bot AB\) suy ra \(NL\parallel AC\)
\(\Delta HAC\) có \(NH = NC\)và \(NL\parallel AC\) nên \(AL = LH\)
Từ đó \(AL = LH = 2.IH\), suy ra \(AH = 4.IH\) và \(AI = 3.IH\).
Do đó \(\frac{{AH}}{{AI}} = \frac{4}{3}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi số cabin của tuyến Vân Sơn là \(x\) (cabin) \(\left( {x \in {\mathbb{Z}^ + }, x < 191} \right)\)
Gọi số cabin của tuyến Chùa Hang là \(y\) (cabin) \(\left( {y \in {\mathbb{Z}^ + }, y < 191} \right)\)
Hai tuyến Vân Sơn và Chùa Hang có tổng cộng 191 cabin nên:
\(x + y = 191\)
Vì số người ở tuyến Vân Sơn nhiều hơn số người ở tuyến Chùa Hang là 350 người (nếu mỗi cabin chứa đủ 10 người) nên:
\(10x - 10y = 350\) hay \(x - y = 35\)
Ta có hệ phương trình
\(\left\{ {\begin{array}{*{20}{c}}{x + y = 191}\\{x - y = 35}\end{array}} \right.\) \( \Leftrightarrow \)\(\left\{ {\begin{array}{*{20}{c}}{x + y = 191}\\{2x = 226}\end{array}} \right.\) \( \Leftrightarrow \)\(\left\{ {\begin{array}{*{20}{c}}{x = 113 (nha\"a n)}\\{y = 78 (nha\"a n)}\end{array}} \right.\)
Vậy tuyến Vân Sơn có 113 cabin tuyến Chùa Hang có 78 cabin.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập