Trong cuộc gặp mặt dặn dò trước khi lên đường tham gia kì thi học sinh giỏi, có 10 bạn trong đội tuyển gồm 2 bạn đến từ lớp 12A, 3 bạn từ lớp 12B, 5 bạn còn lại đến từ 5 lớp khác (mỗi lớp một bạn). Thầy giáo xếp ngẫu nhiên các bạn kể trên ngồi vào một bàn dài có 10 ghế mà mỗi bên có 5 ghế xếp đối diện nhau. Xác suất để không có học sinh nào cùng lớp ngồi đối diện nhau bằng \(\frac{a}{b}\)( với \(\frac{a}{b}\)là phân số tối giản). Tính \(a - b\).

Đáp số : 30

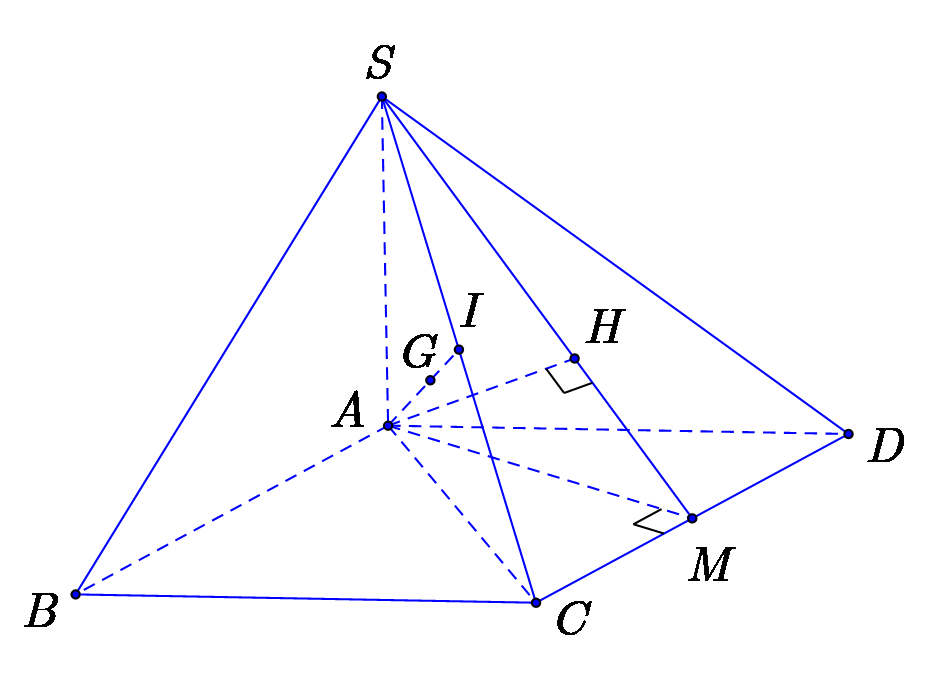
Gọi \(M,I\)lần lượt là trung điểm \(CD,\,SC\).

Theo giả thiết ta có tam giác \(ACD\) đều. Suy ra \(AM = \frac{{AD\sqrt 3 }}{2} = \frac{{\sqrt 3 a}}{2}\).

Kẻ \(AH \bot SM\,\,\left( {H \in SM} \right)\) thì \(AH \bot \left( {SCD} \right)\).

Ta có \(GI = \frac{1}{3}AI\) nên \(d\left( {G,\left( {SCD} \right)} \right) = \frac{1}{3}d\left( {A,\left( {SCD} \right)} \right) = \frac{1}{3}AH\)

\( = \frac{1}{3}.\frac{{AM.SA}}{{\sqrt {A{M^2} + S{A^2}} }} = \frac{1}{3}.\frac{{\frac{{\sqrt 3 a}}{2}.\sqrt 3 a}}{{\sqrt {\frac{{3{a^2}}}{4} + 3{a^2}} }} = \frac{{\sqrt {15} a}}{{15}}\)

Vậy \(d\left( {G,\left( {SCD} \right)} \right) = \frac{{\sqrt {15} a}}{{15}}\).

Đáp án: 34,1

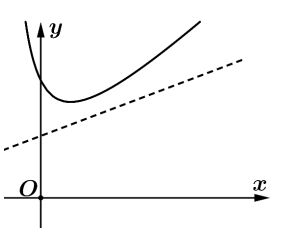
Đồ thị hàm số có tiệm cận đứng \(x =  - b = 1 \Rightarrow b =  - 1\).

Khi đó đồ thị hàm số \(y = \frac{{x + a}}{{x - 1}}\) qua \(\left( {2\,;\,\,3} \right) \Rightarrow 3 = \frac{{2 + a}}{{2 - 1}} \Rightarrow a = 1\); hàm số là  (C).

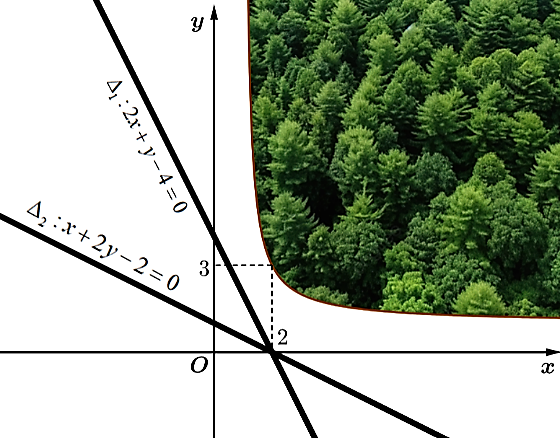
Ta nhận thấy để khoảng cách từ điểm m thuộc khu vườn đến hai đường thẳng là nhỏ nhất thì điểm M phải thuộc đồ thị hàm số.

Gọi \(M\left( {{x_0}\,;\,\,\frac{{{x_0} + 1}}{{{x_0} - 1}}} \right) \in \left( C \right),\,\,{x_0} > 1\). Tổng khoảng cách từ M đến hai đường thẳng \({\Delta _1},\,\,{\Delta _2}\) là

\(d = d\left( {M\,,\,\,{\Delta _1}} \right) + d\left( {M\,,\,\,{\Delta _2}} \right) = \frac{{\left| {2{x_0} + \frac{{{x_0} + 1}}{{{x_0} - 1}} - 4} \right|}}{{\sqrt 5 }} + \frac{{\left| {{x_0} + 2 \cdot \frac{{{x_0} + 1}}{{{x_0} - 1}} - 2} \right|}}{{\sqrt 5 }}\) ;

\(\sqrt 5 d = \left| {\frac{{2x_0^2 - 5{x_0} + 5}}{{{x_0} - 1}}} \right| + \left| {\frac{{x_0^2 - {x_0} + 4}}{{{x_0} - 1}}} \right| = \frac{{2x_0^2 - 5{x_0} + 5}}{{{x_0} - 1}} + \frac{{x_0^2 - {x_0} + 4}}{{{x_0} - 1}}\)

(vì \(\left\{ \begin{array}{l}2x_0^2 - 5{x_0} + 5 > 0\\{x_0} - 1 > 0\\x_0^2 - {x_0} + 4 > 0\end{array} \right.\,,\,\,\forall {x_0} > 1\)).

Đặt \(\sqrt 5 d = \frac{{3x_0^2 - 6{x_0} + 9}}{{{x_0} - 1}} = g\left( x \right)\) với \(x > 1\).

Ta có: \(g'\left( x \right) = \frac{{3x_0^2 - 6{x_0} - 3}}{{{{\left( {{x_0} - 1} \right)}^2}}}\); \(g'\left( x \right) = 0 \Rightarrow 3x_0^2 - 6{x_0} - 3 = 0 \Rightarrow {x_0} = 1 + \sqrt 2  > 1\).

Ta có: .

Dấu đẳng thức xảy ra khi \({x_0} = 1 + \sqrt 2 \)\( \Rightarrow M\left( {1 + \sqrt 2 \,;\,\,1 + \sqrt 2 } \right)\).

Khoảng cách OM trên thực tế là  mét.