Từ điểm \(M\) nằm bên ng̀oài đường tròn tâm \(O\), vẽ hai tiếp tuyến \(MA\) và \(MB\) với đường tròn \((A,B\) là tiếp điểm).

a. Chứng minh tứ giác \(MAOB\) nội tiếp đường tròn.

b. Vẽ đường kinh \(AC\) của \(\left( O \right)\), gọi \(D\) là giao điểm của \(MC\) và \(\left( O \right)\), biết \(D\) khác \(C\). Chứng minh \(M{A^2} = MD.MC\)

c. Hai đoạn thẳng \(AB\) và \(MO\) cắt nhau tại \(H\), kẻ đường kính \(BE\) của \(\left( O \right)\). Chứng minh ba điểm \(E,H,D\) thẳng hàng.

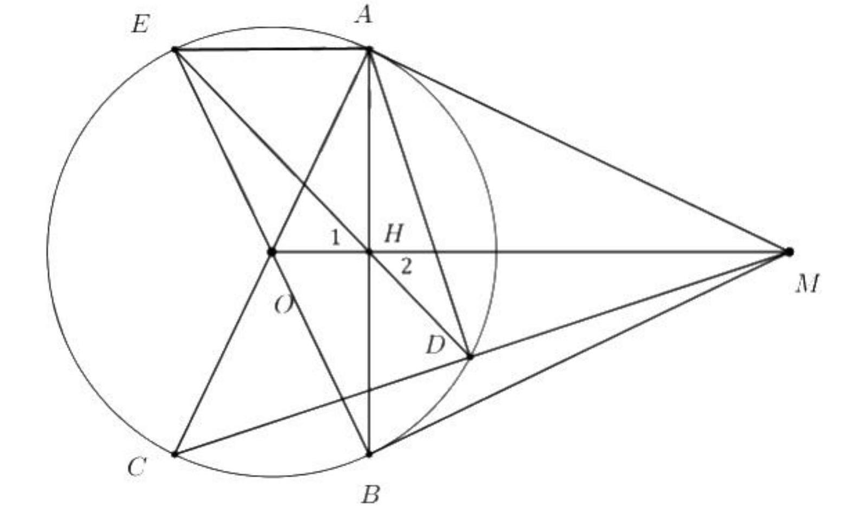
a. Chứng minh tứ giác \(MAOB\) nội tiếp đường tròn.

 Do MA, MB là tiếp tuyến của \(\left( {\rm{O}} \right)\) nên \(MA \bot OA,MB \bot OB\) (tính chất) \( \Rightarrow \widehat {MAO} = \widehat {MBO} = {90^0}\)

\( \Rightarrow \widehat {MAO} + \widehat {MBO} = {90^0} + {90^0} = {180^0}\)

Mà hai góc này ở vị trí đối diện của tứ giác \(MAOB\) nên tứ giác \(MAOB\) nội tiếp (dhnb) (đpcm)

b. Vẽ đường kinh \(AC\) của \(\left( O \right)\), gọi \(D\) là giao điểm của \(MC\) và \(\left( O \right)\), biết \(D\) khác \(C\). Chứng minh \(M{A^2} = MD.MC\)

Xét \(\Delta MAD\) và \(\Delta MCA\) có:

\(\widehat {AMC}\) chung

\(\widehat {MAD} = \widehat {MCA}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn một cung)

 (đpcm)

c. Hai đoạn thẳng \(AB\) và \(MO\) cắt nhau tại \(H\), kẻ đường kính \(BE\) của \(\left( O \right)\). Chứng minh ba điểm \(E,H,D\) thẳng hàng.

Do \({\rm{MA}},{\rm{MB}}\) là 2 tiếp tuyến cắt nhau của \(\left( {\rm{O}} \right)\) nên \({\rm{MA}} = {\rm{MB}}\) (tính chất)

Mà \({\rm{OA}} = {\rm{OB}}\) (bằng bán kính) nên \({\rm{MO}}\) là trung trực của \({\rm{AB}}\) (tính chất)

\( \Rightarrow MO \bot AB\) tại \({\rm{H}}\) và \({\rm{H}}\) là trung điểm của \({\rm{AB}}\)

Khi đó xét tam giác \({\rm{MAO}}\) vuông tại \({\rm{A}}\), đường cao \({\rm{AH}}\) có \(M{A^2} = MH.MO\) (hệ thức lượng trong tam giác vuông)

Mà \(M{A^2} = MC \cdot MD\left( {{\rm{cmt}}} \right)\) nên suy ra \(MH \cdot MO = MD \cdot MC \Leftrightarrow \frac{{MH}}{{MC}} = \frac{{MD}}{{MO}}\)

Xét \(\Delta MHD\) và \(\Delta MCO\) có

\(\widehat {OMC}\) chung

\(\frac{{MH}}{{MC}} = \frac{{MD}}{{MO}}\)

 (c.g.c \() \Rightarrow \widehat {{H_2}} = \widehat {MCO}\) (2 góc tương ứng)

Do \({\rm{BE}}\) đường kính nên \(\widehat {BAE} = {90^0}\) (góc nội tiếp chắn nửa đường tròn)

\( \Rightarrow AE \bot AB\) mà \(AO \bot AB \Rightarrow AE{\rm{//}}AO\)

\[ \Rightarrow {\widehat H_1} = \widehat {AED}\] (so le trong)

Mà \(\widehat {AED} = \widehat {ACD}\) (góc nội tiếp cùng chắn cung \(AD\) )

Từ (1) (2) (3) suy ra \(\widehat {{H_1}} = \widehat {{H_2}}\)

Mà \(\widehat {{H_1}} + \widehat {EHM} = {180^0}\) (2 góc kề bù) \( \Rightarrow \widehat {{H_2}} + \widehat {MHE} = {180^0}\)

\( \Rightarrow E,H,D\) thẳng hàng