Tập nghiệm của bất phương trình bậc hai \({x^2} - 2x + 4 < 0\) là

Gọi \(A\left( {{x_A};{y_A}} \right)\) và \(B\left( {{x_B},{y_B}} \right)\).

Do điểm \(M\left( {2;2} \right)\) là trung điểm của cạnh \(BC\) nên ta có:

\(\left\{ \begin{array}{l}\frac{{{x_B} - 1}}{2} = 2\\\frac{{{y_B} + 2}}{2} = 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_B} = 5\\{y_B} = 2\end{array} \right. \Rightarrow B\left( {5;2} \right)\).

Do \(G\left( {3;1} \right)\) là trọng tâm của tam giác nên ta có:

\(AG = \frac{2}{3}AM \Rightarrow AG = 2GM \Rightarrow \overrightarrow {AG}  = 2\overrightarrow {GM} \)

Mà: \(\overrightarrow {AG}  = \left( {3 - {x_A};1 - {y_A}} \right)\); \(\overrightarrow {GM}  = \left( {2 - 3;2 - 1} \right) = \left( { - 1;\,\,1} \right)\)

Do đó, \(\overrightarrow {AG}  = 2\overrightarrow {GM}  \Leftrightarrow \left\{ \begin{array}{l}3 - {x_A} = 2 \cdot ( - 1)\\1 - {y_A} = 2 \cdot 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_A} = 5\\{y_A} =  - 1\end{array} \right. \Rightarrow A\left( {5; - 1} \right)\).

Đường thẳng \(AB\) có một vectơ chỉ phương \(\overrightarrow {AB}  = \left( {5 - 5;2 - ( - 1)} \right) = \left( {0;3} \right)\)

Do đó, nó có một vectơ pháp tuyến là: \(\overrightarrow n  = \left( { - 3;0} \right)\).

Phương trình tổng quát của đường thẳng \(AB\) đi qua điểm \(A\) và có vectơ pháp tuyến  \(\overrightarrow n  = \left( { - 3;0} \right)\) là \( - 3\left( {x - 5} \right) + 0.\left( {y - ( - 1)} \right) = 0 \Leftrightarrow x - 5 = 0\).

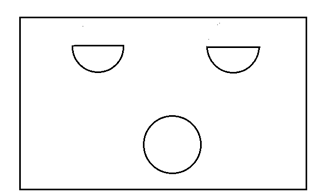
Gọi bán kính của vòng tròn và hai nửa hình tròn tương ứng là \(x\), \(y\) (m) \(\left( {x,y > 0} \right)\).

Chu vi của vòng tròn là: \(2 \cdot 3,14 \cdot x = 6,28x\) (m).

Vì hai nửa hình tròn bằng nhau nên tổng chu vi của hai nửa này bằng tổng chu vi của đường tròn bán kính \(y\) (m) với 2 lần độ dài đường kính của đường tròn đó, do đó chu vi của hai nửa hình tròn là: \(2 \cdot 3,14 \cdot y + 4y = 10,28y\) (m).

Tổng chu vi của chúng là 36 m nên ta có:

\(6,28x + 10,28y = 36 \Rightarrow 6,28x + 10,28y - 36 = 0 \Leftrightarrow 1,57x + 2,57y - 9 = 0\).

Diện tích của vòng tròn là: \(3,14{x^2}\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\).

Diện tích của hai nửa hình tròn là: \(2 \cdot \frac{1}{2} \cdot 3,14 \cdot {y^2} = 3,14{y^2}\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\).

Gọi tổng diện tích của chúng là \(S\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\). Khi đó ta có:

\(S = 3,14{x^2} + 3,14{y^2}\, \Rightarrow {x^2} + {y^2}\, = \frac{S}{{3,14}}\).

Trong mặt phẳng tọa độ \(Oxy\), xét đường tròn \(\left( C \right):{x^2} + {y^2} = \frac{S}{{3,14}}\) có tâm \(O\left( {0;0} \right)\) và bán kính \(R = \sqrt {\frac{S}{{3,14}}} \)  và đường thẳng \(\Delta :1,57x + 2,57y - 9 = 0\).

Khi đó bài toán được chuyển thành: Tìm \(R\) nhỏ nhất để \(\left( C \right)\) và \(\Delta \) có ít nhất một điểm chung, với hoành độ và tung độ đều là các số dương.

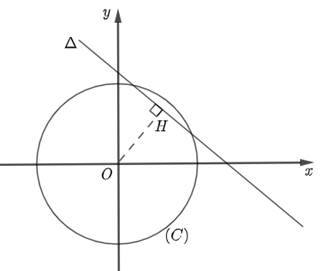
Bài toán trên tương đương với \(\Delta \) tiếp xúc với \(\left( C \right)\), đồng thời khi đó điểm \(M\) trùng với điểm \(H\) là hình chiếu vuông góc của \(O\) trên \(\Delta \).

Ta có: \(OH \bot \Delta  \Rightarrow \overrightarrow {{u_{OH}}}  = \overrightarrow {{n_\Delta }}  = \left( {1,57;2,57} \right)\)

Suy ra đường thẳng \(OH\) có một vectơ pháp tuyến là: \(\overrightarrow {{n_{OH}}}  = \left( { - 2,57;1,57} \right)\)

Phương trình đường thẳng \(OH\) là:

\( - 2,57\left( {x - 0} \right) + 1,57\left( {y - 0} \right) = 0 \Leftrightarrow 2,57x - 1,57y = 0\).

Điểm \(H\) là giao điểm của đường thẳng \(OH\) và đường thẳng \(\Delta \) nên tọa độ của \(H\)là nghiệm của hệ phương trình

\(\left\{ \begin{array}{l}2,57x - 1,57y = 0\\1,57x + 2,57y - 9 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \approx 1,56\\y \approx 2,55\end{array} \right.\).

Vậy bán kính vòng tròn xấp xỉ bằng 1,56 m và bán kính hai nửa hình tròn xấp xỉ bằng 2,55 m thì thỏa mãn yêu cầu bài toán.