Giải pháp chủ yếu để tăng doanh thu từ khách du lịch quốc tế ở nước ta hiện nay là
Giải pháp chủ yếu để tăng doanh thu từ khách du lịch quốc tế ở nước ta hiện nay là
Quảng cáo
Trả lời:
Đáp án đúng là D
Phương pháp giải
Dựa vào lí thuyết phần Thương mại và du lịch.
Lời giải
Giải pháp chủ yếu để tăng doanh thu từ khách du lịch quốc tế ở nước ta hiện nay là hiện đại hóa cơ sở vật chất, đa dạng hóa sản phẩm du lịch.
- Hiện đại hóa cơ sở vật chất:
+ Nâng cấp các sân bay, cảng biển, đường giao thông để thuận tiện cho việc di chuyển của du khách.
+ Xây dựng và nâng cấp các cơ sở lưu trú, nhà hàng, khu vui chơi giải trí đạt tiêu chuẩn quốc tế.
+ Tăng cường hệ thống thông tin liên lạc, internet để phục vụ nhu cầu của du khách.
- Đa dạng hóa sản phẩm du lịch:
+ Khai thác các loại hình du lịch mới như du lịch sinh thái, du lịch văn hóa, du lịch khám phá, du lịch MICE (hội họp, sự kiện, hội nghị, triển lãm).
+ Phát triển các sản phẩm du lịch đặc trưng của từng vùng miền, tạo ra sự khác biệt và thu hút khách du lịch.
+ Tổ chức các sự kiện văn hóa, thể thao, lễ hội để thu hút du khách.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là "10"
Phương pháp giải
- Thành phần trong đinh sắt gồm sắt nguyên chất và gỉ sắt và cả hai đều phản ứng với dung dịch H2SO4 loãng và đều chuyển hóa hoàn toàn về muối sắt sulfate vì H2SO4 dùng dư.
- Khi cho dung dịch BaCl2 dư vào thì dung dịch X thì có kết tủa BaSO4 được sinh ra.
- Nhỏ từ từ dung dịch KMnO4 0,02M vào 5,00 mL dung dịch X thì muối sắt(II) sulfate.
Lời giải
+) nBaSO4 = 0,0021 ⟹ nH2SO4 pư = 0,0021:2 = 0,00105
+) nKMnO4 = 1,8.10-4
2KMnO4 + 10.FeSO4 + 8.H2SO4 ⟶ 5.Fe2(SO4)3 + 2MnSO4 + K2SO4 + 8.H2O
1,8.10-4 ⟶ 9.10-4
+) BTNT S: nH2SO4 = nFeSO4 + 3.nFe2(SO4)3 ⟹ nFe2(SO4)3 = 5.10-5
⟹ nFe bị oxi hóa thành Fe2O3 = 2.5.10-5 = 10-4
⟹ ntổng số mol Fe = nFeSO4 + 2.nFe2(SO4)3 = 10-3
⟹ %Fe = (10-4/10-3).100% = 10%
Câu 2
Lời giải
Đáp án đúng là B
Phương pháp giải
Lời giải
Hiện tượng quan sát được khi cho vào propyne là thu được kết tủa vàng:
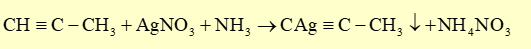
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
