Đọc đoạn trích và trả lời câu hỏi dưới đây.

     Mười ba người tại đây, sở dĩ trôi dạt đến đây, là bởi cũng đã như con thiêu thân bay vào đống lửa, cho nên mới bị quáng mắt về những ánh sáng của kinh thành. Mụ chủ hàng cơm đã chứa chấp họ trong những xó sân. Ban ngày họ ra ngồi bày hàng ở ngã ba, ngã bảy. Trong khi chờ cho có việc, họ có mấy đồng xu cứ ăn hết dần. Đến cái ngày mà túi cạn mà việc chưa có, mà không ai thí cho đồng chinh hay bát cháo, tất là họ phải sinh ra liều mạng, có những lá gan to. Đàn bà sẽ đi đến Dục tình. Đàn ông sẽ đi đến Hình phạt. Trước khi đi đến cái ấy, hiện giờ thì họ bình tĩnh nằm chờ cái sóng gió là ngày mai.

(Vũ Trọng Phụng, Ánh sáng kinh thành, in trong Phóng sự, NXB Văn học, Hà Nội, 2016)

Biện pháp tu từ được sử dụng trong câu văn “Mười ba người tại đây, sở dĩ trôi dạt đến đây, là bởi cũng đã như con thiêu thân bay vào đống lửa, cho nên mới bị quáng mắt về những ánh sáng của kinh thành.” là gì?

Đáp án đúng là A

Phương pháp giải

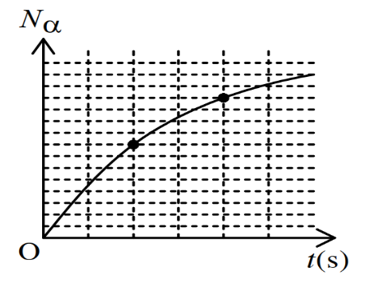
Sử dụng định luật phóng xạ về số hạt còn lại sau thời gian t: \(N = {N_0}{2^{ - \frac{t}{T}}}\)

Lời giải

Số hạt đã phân rã trong thời gian t:

\({N_\alpha } = {N_0}.\left( {1 - {2^{\frac{{ - t}}{T}}}} \right) \Rightarrow \left\{ {\begin{array}{*{20}{l}}{8\^o = {N_0}.\left( {1 - {2^{\frac{{ - 8}}{T}}}} \right)}\\{12\^o = {N_0}.\left( {1 - {2^{\frac{{ - 16}}{T}}}} \right)}\end{array} \Rightarrow \frac{8}{{12}}} \right. = \frac{{1 - {2^{\frac{{ - 8}}{T}}}}}{{1 - {2^{\frac{{ - 16}}{T}}}}} \Rightarrow T = 8s\)

Đáp án đúng là "5"

Phương pháp giải

Tính chất của tích phân.

Lời giải

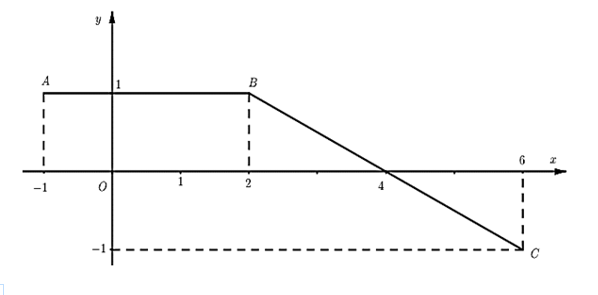
Từ đồ thị của hàm số ta xác định được \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{{\rm{1}}\,\,{\rm{khi}} - 1 \le x < 2}\\{ - \frac{1}{2}x + 2\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\).

Do \(F\) là nguyên hàm của \(f\) nên \(F\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{x + {C_1}\,\,{\rm{khi}}\,\, - 1 \le x < 2}\\{ - \frac{1}{4}{x^2} + 2x + {C_2}\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\).

Ta có \(F\left( { - 1} \right) =  - 1 \Leftrightarrow  - 1 + {C_1} =  - 1 \Leftrightarrow {C_1} = 0\).

Hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;6} \right] \Rightarrow F\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;6} \right]\)

\( \Rightarrow F\left( x \right)\) liên tục tại \(x = 2\)

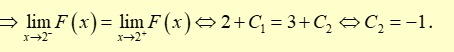
Suy ra \(F\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{x + {C_1}\,\,{\rm{khi}}\,\, - 1 \le x < 2}\\{ - \frac{1}{4}{x^2} + 2x - 1\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\). Vậy \(F\left( 4 \right) + F\left( 6 \right) = 5\).