Đọc đoạn thơ và trả lời câu hỏi dưới đây.

Chúng ta thương những ngày ít gió và nhiều mây

những ngày chỉ nói với nhau bằng ánh mắt

những ngày chỉ cần tựa vai đã thấy lòng thanh thản

những ngày mà nỗi cô đơn cũng cần như hạt muối mặn

nêm vào những bình yên…

(Nguyễn Phong Việt, Đã đi qua thương nhớ, In trong Đi qua thương nhớ, NXB Hội Nhà văn, Hà Nội, 2016)

Theo đoạn trích, việc nêm “cô đơn” vào “những bình yên” cho thấy điều gì?

Đáp án đúng là A

Phương pháp giải

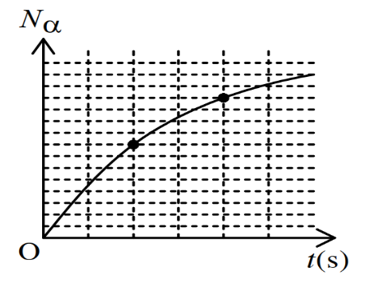
Sử dụng định luật phóng xạ về số hạt còn lại sau thời gian t: \(N = {N_0}{2^{ - \frac{t}{T}}}\)

Lời giải

Số hạt đã phân rã trong thời gian t:

\({N_\alpha } = {N_0}.\left( {1 - {2^{\frac{{ - t}}{T}}}} \right) \Rightarrow \left\{ {\begin{array}{*{20}{l}}{8\^o = {N_0}.\left( {1 - {2^{\frac{{ - 8}}{T}}}} \right)}\\{12\^o = {N_0}.\left( {1 - {2^{\frac{{ - 16}}{T}}}} \right)}\end{array} \Rightarrow \frac{8}{{12}}} \right. = \frac{{1 - {2^{\frac{{ - 8}}{T}}}}}{{1 - {2^{\frac{{ - 16}}{T}}}}} \Rightarrow T = 8s\)

Đáp án đúng là "5"

Phương pháp giải

Tính chất của tích phân.

Lời giải

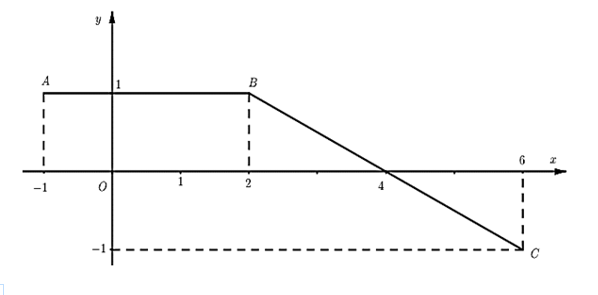
Từ đồ thị của hàm số ta xác định được \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{{\rm{1}}\,\,{\rm{khi}} - 1 \le x < 2}\\{ - \frac{1}{2}x + 2\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\).

Do \(F\) là nguyên hàm của \(f\) nên \(F\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{x + {C_1}\,\,{\rm{khi}}\,\, - 1 \le x < 2}\\{ - \frac{1}{4}{x^2} + 2x + {C_2}\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\).

Ta có \(F\left( { - 1} \right) =  - 1 \Leftrightarrow  - 1 + {C_1} =  - 1 \Leftrightarrow {C_1} = 0\).

Hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;6} \right] \Rightarrow F\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;6} \right]\)

\( \Rightarrow F\left( x \right)\) liên tục tại \(x = 2\)

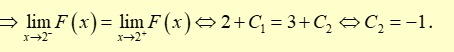
Suy ra \(F\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{x + {C_1}\,\,{\rm{khi}}\,\, - 1 \le x < 2}\\{ - \frac{1}{4}{x^2} + 2x - 1\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\). Vậy \(F\left( 4 \right) + F\left( 6 \right) = 5\).