Đọc đoạn trích và trả lời câu hỏi dưới đây.

THẦY TRIẾT: (Vừa đi vừa đỉnh lại miếng vải đeo ở cổ áo) – Ta vào bài học nào.

ÔNG GIUỐC-ĐANH: – Chà! Thầy ạ, tôi rất buồn lòng thấy thầy bị họ đánh đập.

THẦY TRIẾT: – Không hề gì. Một nhà hiền triết biết tiếp thu sự vật một cách phải lẽ; để rồi tôi sẽ soạn một bài văn trào phúng theo Juvenan đả kích cho họ tơi bời một phen. Thôi ta hãy gác chuyện đó. Ngài muốn học gì?

ÔNG GIUỐC-ĐANH: – Học tất cả những cái gì tôi có thể học được, vì tôi hết sức thèm

muốn được trở thành người bác học, và tôi tức giận rằng bố mẹ tôi đã không cho tôi học hành tử tế tất cả các khoa học, khi tôi còn trẻ tuổi.

THẦY TRIẾT: – Nam sine doctrina vita quasi mortis imago. Ngài hiểu câu đó chứ, và hẳn là ngài biết tiếng La-tinh chứ?

ÔNG GIUỐC-ĐANH: – Có, nhưng thầy cứ làm như tôi không biết. Thầy cứ giảng cho

Di tôi cái nghĩa của câu đó đi.

THẦY TRIẾT: – Câu đó có nghĩa là không có học thức thì đời sống cũng gần như hình ảnh của cái chết.

(Molière, Trích Trưởng giả học làm sang, NXB Sân khấu, Hà Nội, 2006)  

Ông Giuốc-đanh giận bố mẹ mình vì lí do gì?

Đáp án đúng là A

Phương pháp giải

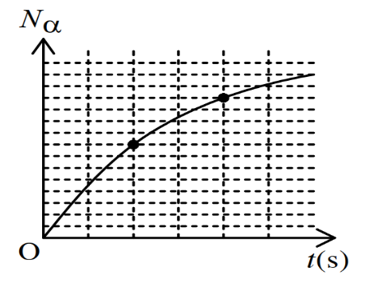
Sử dụng định luật phóng xạ về số hạt còn lại sau thời gian t: \(N = {N_0}{2^{ - \frac{t}{T}}}\)

Lời giải

Số hạt đã phân rã trong thời gian t:

\({N_\alpha } = {N_0}.\left( {1 - {2^{\frac{{ - t}}{T}}}} \right) \Rightarrow \left\{ {\begin{array}{*{20}{l}}{8\^o = {N_0}.\left( {1 - {2^{\frac{{ - 8}}{T}}}} \right)}\\{12\^o = {N_0}.\left( {1 - {2^{\frac{{ - 16}}{T}}}} \right)}\end{array} \Rightarrow \frac{8}{{12}}} \right. = \frac{{1 - {2^{\frac{{ - 8}}{T}}}}}{{1 - {2^{\frac{{ - 16}}{T}}}}} \Rightarrow T = 8s\)

Đáp án đúng là "5"

Phương pháp giải

Tính chất của tích phân.

Lời giải

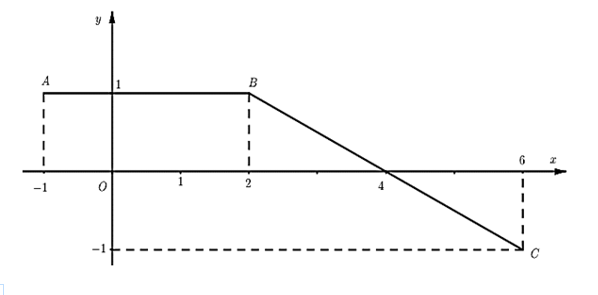
Từ đồ thị của hàm số ta xác định được \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{{\rm{1}}\,\,{\rm{khi}} - 1 \le x < 2}\\{ - \frac{1}{2}x + 2\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\).

Do \(F\) là nguyên hàm của \(f\) nên \(F\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{x + {C_1}\,\,{\rm{khi}}\,\, - 1 \le x < 2}\\{ - \frac{1}{4}{x^2} + 2x + {C_2}\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\).

Ta có \(F\left( { - 1} \right) =  - 1 \Leftrightarrow  - 1 + {C_1} =  - 1 \Leftrightarrow {C_1} = 0\).

Hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;6} \right] \Rightarrow F\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;6} \right]\)

\( \Rightarrow F\left( x \right)\) liên tục tại \(x = 2\)

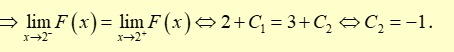
Suy ra \(F\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{x + {C_1}\,\,{\rm{khi}}\,\, - 1 \le x < 2}\\{ - \frac{1}{4}{x^2} + 2x - 1\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\). Vậy \(F\left( 4 \right) + F\left( 6 \right) = 5\).