Diện tích mặt pittông là 150cm² nằm cách đáy của xilanh đoạn 30cm, khối lượng khí ở t = 25^oC, p =10⁵Pa. Khi nhận được năng lượng do 5g xăng bị đốt cháy tỏa ra, khí dãn nở ở áp suất không đổi, nhiệt độ của nó tăng thêm 50^oC. Hiệu suất của quá trình dãn khí là bao nhiêu? Biết rằng chỉ có 10% năng lượng của xăng lá có ích, năng suất tỏa nhiệt của xăng là q = 4,4.10⁷J/kg. Coi khí là lý tưởng.

Đáp án đúng là A

Phương pháp giải

Sử dụng định luật phóng xạ về số hạt còn lại sau thời gian t: \(N = {N_0}{2^{ - \frac{t}{T}}}\)

Lời giải

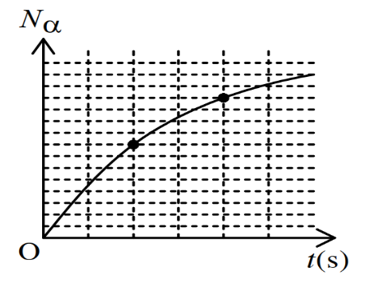
Số hạt đã phân rã trong thời gian t:

\({N_\alpha } = {N_0}.\left( {1 - {2^{\frac{{ - t}}{T}}}} \right) \Rightarrow \left\{ {\begin{array}{*{20}{l}}{8\^o = {N_0}.\left( {1 - {2^{\frac{{ - 8}}{T}}}} \right)}\\{12\^o = {N_0}.\left( {1 - {2^{\frac{{ - 16}}{T}}}} \right)}\end{array} \Rightarrow \frac{8}{{12}}} \right. = \frac{{1 - {2^{\frac{{ - 8}}{T}}}}}{{1 - {2^{\frac{{ - 16}}{T}}}}} \Rightarrow T = 8s\)

Đáp án đúng là "5"

Phương pháp giải

Tính chất của tích phân.

Lời giải

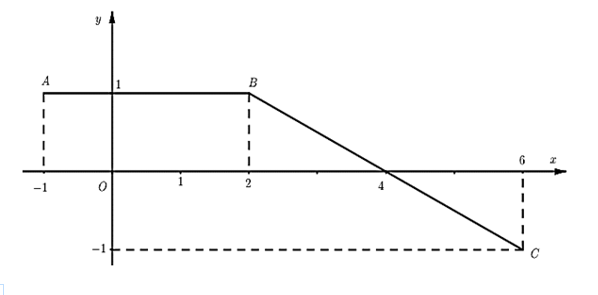
Từ đồ thị của hàm số ta xác định được \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{{\rm{1}}\,\,{\rm{khi}} - 1 \le x < 2}\\{ - \frac{1}{2}x + 2\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\).

Do \(F\) là nguyên hàm của \(f\) nên \(F\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{x + {C_1}\,\,{\rm{khi}}\,\, - 1 \le x < 2}\\{ - \frac{1}{4}{x^2} + 2x + {C_2}\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\).

Ta có \(F\left( { - 1} \right) =  - 1 \Leftrightarrow  - 1 + {C_1} =  - 1 \Leftrightarrow {C_1} = 0\).

Hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;6} \right] \Rightarrow F\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;6} \right]\)

\( \Rightarrow F\left( x \right)\) liên tục tại \(x = 2\)

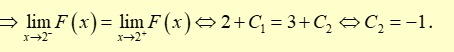
Suy ra \(F\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{x + {C_1}\,\,{\rm{khi}}\,\, - 1 \le x < 2}\\{ - \frac{1}{4}{x^2} + 2x - 1\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\). Vậy \(F\left( 4 \right) + F\left( 6 \right) = 5\).