Trong y học người ta sử dụng các nguồn bức xạ ion hoá chiếu xạ để điều trị bệnh với mục đích tiêu diệt những tế bào, tổ chức bệnh lý với nguyên tắc tránh tối đa những tổn thương cho tổ chức, cơ quan lành bảo đảm chức năng sống bình thường của cơ thể. Điều trị bệnh bằng nguồn bức xạ ion hoá có thể thực hiện bằng các phương thức sau:

- Xạ trị chiếu ngoài cơ thể: Nguồn bức xạ là các máy phát tia qua bộ phận chuẩn trực chiếu xạ từ ngoài cơ thể vào bộ phận cần điều trị.

- Xạ trị áp sát: Các đồng vị phóng xạ như Radium-226, Cesi -137 được tạo thành các nguồn dạng kim, que, hạt, bút , sợi hoặc các đồng vị phóng xạ ngắn ngày khác như Ytrium-90, Holmium-166 gắn trên các giá đỡ, bóng, tấm áp để đưa vào các hốc tự nhiên, ống tiêu hoá, mạch máu áp sát tổn thương hoặc dán áp sát trên da vùng khối u để chiếu xạ điều trị.

- Xạ trị chiếu trong: Là phương thức điều trị bằng cách đưa vào cơ thể một đồng vị phóng xạ nguồn hở dưới dạng thuốc qua đường uống, đường tiêm hoặc truyền qua động mạch-tĩnh mạch. Khi vào cơ thể các hạt nhân phóng xạ sẽ phát huy các hiệu quả điều trị theo nhiều cách khác nhau.

Tia nào sau đây không phải tia phóng xạ?

Đáp án đúng là A

Phương pháp giải

Sử dụng định luật phóng xạ về số hạt còn lại sau thời gian t: \(N = {N_0}{2^{ - \frac{t}{T}}}\)

Lời giải

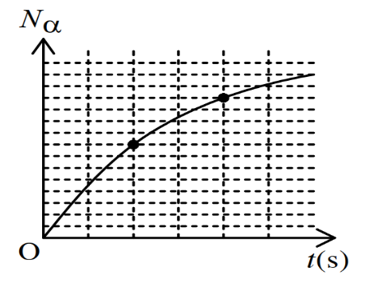
Số hạt đã phân rã trong thời gian t:

\({N_\alpha } = {N_0}.\left( {1 - {2^{\frac{{ - t}}{T}}}} \right) \Rightarrow \left\{ {\begin{array}{*{20}{l}}{8\^o = {N_0}.\left( {1 - {2^{\frac{{ - 8}}{T}}}} \right)}\\{12\^o = {N_0}.\left( {1 - {2^{\frac{{ - 16}}{T}}}} \right)}\end{array} \Rightarrow \frac{8}{{12}}} \right. = \frac{{1 - {2^{\frac{{ - 8}}{T}}}}}{{1 - {2^{\frac{{ - 16}}{T}}}}} \Rightarrow T = 8s\)

Đáp án đúng là "5"

Phương pháp giải

Tính chất của tích phân.

Lời giải

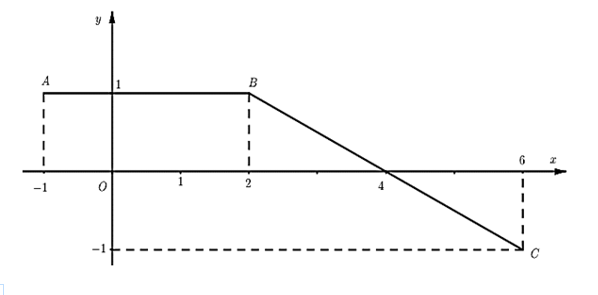
Từ đồ thị của hàm số ta xác định được \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{{\rm{1}}\,\,{\rm{khi}} - 1 \le x < 2}\\{ - \frac{1}{2}x + 2\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\).

Do \(F\) là nguyên hàm của \(f\) nên \(F\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{x + {C_1}\,\,{\rm{khi}}\,\, - 1 \le x < 2}\\{ - \frac{1}{4}{x^2} + 2x + {C_2}\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\).

Ta có \(F\left( { - 1} \right) =  - 1 \Leftrightarrow  - 1 + {C_1} =  - 1 \Leftrightarrow {C_1} = 0\).

Hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;6} \right] \Rightarrow F\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;6} \right]\)

\( \Rightarrow F\left( x \right)\) liên tục tại \(x = 2\)

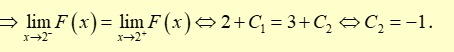
Suy ra \(F\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{x + {C_1}\,\,{\rm{khi}}\,\, - 1 \le x < 2}\\{ - \frac{1}{4}{x^2} + 2x - 1\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\). Vậy \(F\left( 4 \right) + F\left( 6 \right) = 5\).