Mô phân sinh là các tế bào chưa phân hóa, có khả năng phân chia liên tục để tạo ra các tế bào mới. Loại mô phân sinh nào sau đây chỉ có ở thực vật một lá mầm mà không có ở thực vật hai lá mầm?

  

Đáp án đúng là A

Phương pháp giải

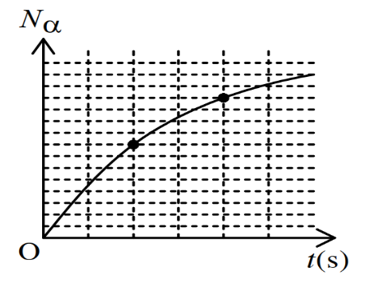
Sử dụng định luật phóng xạ về số hạt còn lại sau thời gian t: \(N = {N_0}{2^{ - \frac{t}{T}}}\)

Lời giải

Số hạt đã phân rã trong thời gian t:

\({N_\alpha } = {N_0}.\left( {1 - {2^{\frac{{ - t}}{T}}}} \right) \Rightarrow \left\{ {\begin{array}{*{20}{l}}{8\^o = {N_0}.\left( {1 - {2^{\frac{{ - 8}}{T}}}} \right)}\\{12\^o = {N_0}.\left( {1 - {2^{\frac{{ - 16}}{T}}}} \right)}\end{array} \Rightarrow \frac{8}{{12}}} \right. = \frac{{1 - {2^{\frac{{ - 8}}{T}}}}}{{1 - {2^{\frac{{ - 16}}{T}}}}} \Rightarrow T = 8s\)

Đáp án đúng là "5"

Phương pháp giải

Tính chất của tích phân.

Lời giải

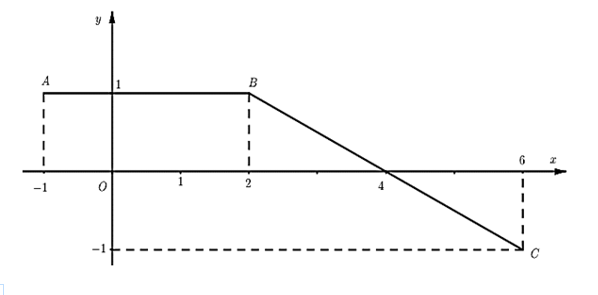
Từ đồ thị của hàm số ta xác định được \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{{\rm{1}}\,\,{\rm{khi}} - 1 \le x < 2}\\{ - \frac{1}{2}x + 2\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\).

Do \(F\) là nguyên hàm của \(f\) nên \(F\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{x + {C_1}\,\,{\rm{khi}}\,\, - 1 \le x < 2}\\{ - \frac{1}{4}{x^2} + 2x + {C_2}\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\).

Ta có \(F\left( { - 1} \right) =  - 1 \Leftrightarrow  - 1 + {C_1} =  - 1 \Leftrightarrow {C_1} = 0\).

Hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;6} \right] \Rightarrow F\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;6} \right]\)

\( \Rightarrow F\left( x \right)\) liên tục tại \(x = 2\)

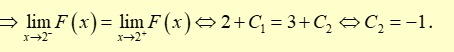
Suy ra \(F\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{x + {C_1}\,\,{\rm{khi}}\,\, - 1 \le x < 2}\\{ - \frac{1}{4}{x^2} + 2x - 1\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\). Vậy \(F\left( 4 \right) + F\left( 6 \right) = 5\).