Choose A, B, C or D to make a complete dialogue for each question.
a. "You need to consider both benefits and challenges before undertaking this role."
b. "Do you think you might regret it if you decide not to take this opportunity?"
c. "I’m a bit worried about balancing this with my studies, but I think I could learn a lot."
d. "I genuinely feel that stepping up as a leader could help me grow and make a difference for my team."
e. "I’m still unsure, but there’s something about this challenge that feels exciting, and I’m leaning toward accepting it."
f. "Have you thought about how you’ll manage the additional workload along with your other commitments?"
Quảng cáo
Trả lời:
Đáp án đúng là C
Phương pháp giải
Sắp xếp hội thoại
Lời giải
Thứ tự đúng: C. d-f-c-b-e-a
Hội thoại hoàn chỉnh:
1 - d. "I genuinely feel that stepping up as a leader could help me grow and make a difference for my team." – Begin by expressing a personal motivation for taking on the role.
2 - f. "Have you thought about how you’ll manage the additional workload along with your other commitments?" – Raise concerns about the practical challenges.
3 - c. "I’m a bit worried about balancing this with my studies, but I think I could learn a lot." – Acknowledge the concern while highlighting the opportunity for growth.
4 - b. "Do you think you might regret it if you decide not to take this opportunity?" – Encourage deeper reflection on the consequences of the decision.
5 - e. "I’m still unsure, but there’s something about this challenge that feels exciting, and I’m leaning toward accepting it." – Reveal uncertainty while expressing excitement about the challenge.
6 - a. "You need to consider both benefits and challenges before undertaking this role." – Conclude with practical advice to weigh the pros and cons.
Tạm dịch hội thoại:
1 - d. "Tôi thực sự cảm thấy rằng việc trở thành người lãnh đạo có thể giúp tôi phát triển và tạo ra sự khác biệt cho đội của mình." – Bắt đầu bằng cách bày tỏ động lực cá nhân.
2 - f. "Bạn đã nghĩ về cách quản lý khối lượng công việc bổ sung cùng với các cam kết khác chưa?" – Đặt vấn đề về những thách thức thực tế.
3 - c. "Tôi hơi lo lắng về việc cân bằng việc này với việc học, nhưng tôi nghĩ rằng mình có thể học được rất nhiều." – Thừa nhận lo ngại nhưng nhấn mạnh cơ hội phát triển.
4 - b. "Bạn có nghĩ rằng bạn sẽ hối tiếc nếu không nắm lấy cơ hội này không?" – Khuyến khích suy nghĩ sâu hơn về hậu quả của quyết định.
5 - e. "Tôi vẫn chưa chắc chắn, nhưng có điều gì đó về thử thách này khiến tôi thấy hào hứng, và tôi đang nghiêng về việc chấp nhận nó." – Thể hiện sự không chắc chắn nhưng nhấn mạnh sự phấn khích.
6 - a. "Bạn cần cân nhắc cả lợi ích và thách thức trước khi đảm nhận vai trò này." – Kết thúc bằng lời khuyên thực tế để cân nhắc ưu và nhược điểm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là A
Phương pháp giải
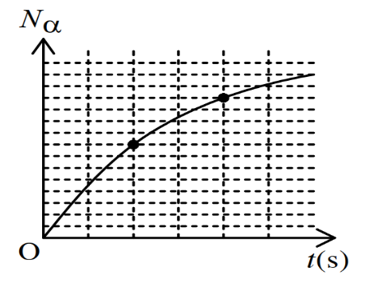
Sử dụng định luật phóng xạ về số hạt còn lại sau thời gian t: \(N = {N_0}{2^{ - \frac{t}{T}}}\)
Lời giải
Số hạt đã phân rã trong thời gian t:
\({N_\alpha } = {N_0}.\left( {1 - {2^{\frac{{ - t}}{T}}}} \right) \Rightarrow \left\{ {\begin{array}{*{20}{l}}{8\^o = {N_0}.\left( {1 - {2^{\frac{{ - 8}}{T}}}} \right)}\\{12\^o = {N_0}.\left( {1 - {2^{\frac{{ - 16}}{T}}}} \right)}\end{array} \Rightarrow \frac{8}{{12}}} \right. = \frac{{1 - {2^{\frac{{ - 8}}{T}}}}}{{1 - {2^{\frac{{ - 16}}{T}}}}} \Rightarrow T = 8s\)
Lời giải
Đáp án đúng là "5"
Phương pháp giải
Tính chất của tích phân.
Lời giải
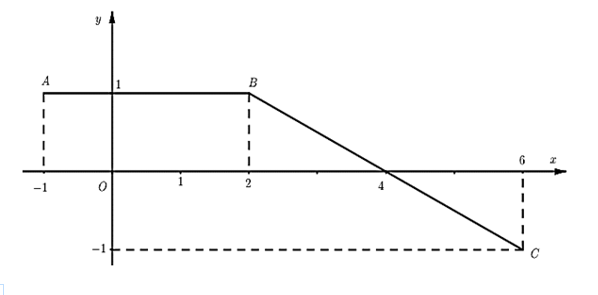
Từ đồ thị của hàm số ta xác định được \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{{\rm{1}}\,\,{\rm{khi}} - 1 \le x < 2}\\{ - \frac{1}{2}x + 2\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\).
Do \(F\) là nguyên hàm của \(f\) nên \(F\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{x + {C_1}\,\,{\rm{khi}}\,\, - 1 \le x < 2}\\{ - \frac{1}{4}{x^2} + 2x + {C_2}\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\).
Ta có \(F\left( { - 1} \right) = - 1 \Leftrightarrow - 1 + {C_1} = - 1 \Leftrightarrow {C_1} = 0\).
Hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;6} \right] \Rightarrow F\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;6} \right]\)
\( \Rightarrow F\left( x \right)\) liên tục tại \(x = 2\)
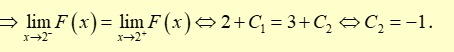
Suy ra \(F\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{x + {C_1}\,\,{\rm{khi}}\,\, - 1 \le x < 2}\\{ - \frac{1}{4}{x^2} + 2x - 1\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\). Vậy \(F\left( 4 \right) + F\left( 6 \right) = 5\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.