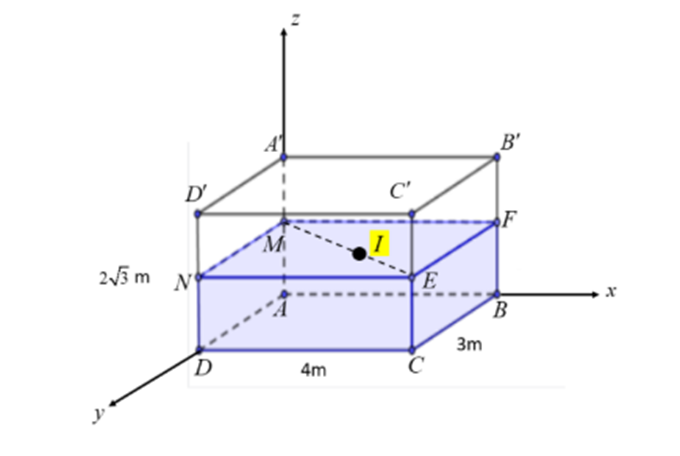
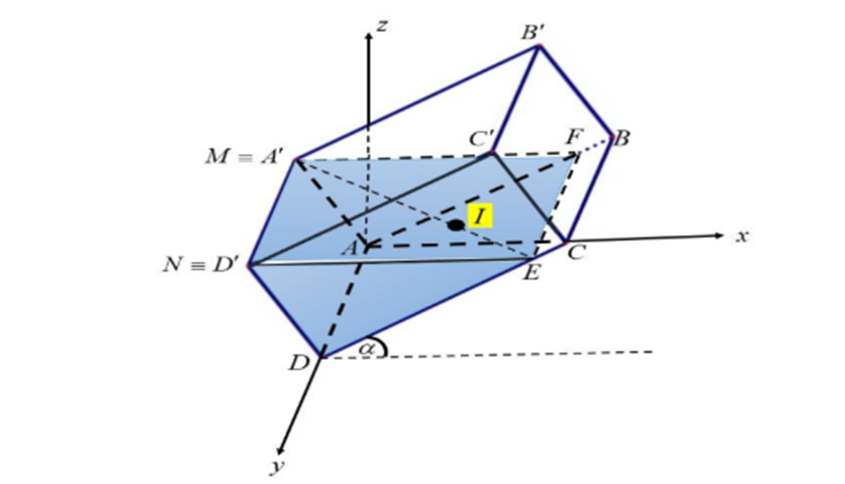
Cho khối chóp \(S.ABC\) được đặt vào trong hệ trục tọa độ \(Oxyz\) với \(B = (0;6;0)\), \(C = (8;0;0)\), \(A\) là điểm trên mặt \((Oxy)\) và \(S\) là điểm nằm trên trục \(Oz\) sao cho \(\overrightarrow {AS} = - \frac{1}{{12}}[\overrightarrow {AB} ,\overrightarrow {AC} ]\). Tính thể tích của khối chóp \(S.ABC\). (Làm tròn đến hàng đơn vị).
Quảng cáo
Trả lời:
Đáp án:
Gọi tọa độ điểm \(A\) là \(A({x_A};{y_A};0)\) (do \(A\) nằm trên mặt phẳng \((Oxy)\)).
Gọi tọa độ điểm \(S\) là \(S(0;0;{z_S})\) (do \(S\) nằm trên trục \(Oz\)).
Ta có: \(\overrightarrow {AB} = ( - {x_A};6 - {y_A};0)\)
\(\overrightarrow {AC} = (8 - {x_A}; - {y_A};0)\)
\(\overrightarrow {AS} = ( - {x_A}; - {y_A};{z_S})\)
\([\overrightarrow {AB} ,\overrightarrow {AC} ] = (0;0;6{x_A} + 8{y_A} - 48)\)
Theo giả thiết, ta có \(\overrightarrow {AS} = - \frac{1}{{12}}[\overrightarrow {AB} ,\overrightarrow {AC} ]\)\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{ - {x_A} = 0}\\{ - {y_A} = 0}\\{{z_S} = - \frac{1}{{12}}(6{x_A} + 8{y_A} - 48)}\end{array}} \right.\)
Từ hai phương trình đầu, ta suy ra \({x_A} = 0\) và \({y_A} = 0\).
Vậy điểm \(A\) trùng với gốc tọa độ \(O\), tức là \(A(0;0;0)\).
Thay \({x_A} = 0\) và \({y_A} = 0\) vào phương trình thứ ba, ta được: \({z_S} = 4\)
Vậy điểm \(S\) có tọa độ là \(S(0;0;4)\).
Khi đó, các đỉnh của khối chóp là \(A(0;0;0)\), \(B(0;6;0)\), \(C(8;0;0)\) và \(S(0;0;4)\).
Ta nhận thấy \(A \equiv O,B \in Oy,C \in Ox,S \in Oz\); \(AC = 8;AB = 6;AS = 4\).
Do đó: \(AB,AC,AS\) đôi một vuông góc.
Suy ra \({V_{S.ABC}} = \frac{1}{6} \cdot AC.AB.AS = \frac{1}{6} \cdot 8.6 \cdot 4 = 8 \cdot 4 = 32\)(đơn vị thể tích).
Làm tròn đến hàng đơn vị, thể tích là \(32\).
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \((\alpha )\) là mặt phẳng qua \(A\) và vuông góc với giao tuyến của hai mặt phẳng \((P),(Q).\)
Ta có: \({\vec n_P} = (1;1;0),{\vec n_Q} = (1;0; - 1) \Rightarrow {\vec n_\alpha } = {\vec n_Q} \times {\vec n_P} = (1; - 1;1) \Rightarrow (\alpha ):x - y + z - 3 = 0.\)
Gọi \(H,K\) lần lượt hình chiếu vuông góc của \(A\) lên \((P),(Q).\) Theo đề bài, ta có
\(AH = d(A,(P)) = 2;AK = d(A,(Q)) = 1;\cos \left( {\widehat {(P),(Q)}} \right) = \frac{{\left| {{{\vec n}_P}.{{\vec n}_Q}} \right|}}{{|{{\vec n}_P}|.|{{\vec n}_Q}|}} = \frac{1}{2} \Rightarrow \left( {\widehat {(P),(Q)}} \right) = 60^\circ .\)
Gọi \(a = (\alpha ) \cap (P),b = (\alpha ) \cap (Q),E = a \cap b \Rightarrow E \in (P) \cap (Q).\) Khi đó, trong mặt phẳng \((\alpha )\) ta có tứ giác \(HAKE\) như hình vẽ.
![Mái nhà tranh của ông F được đặt vào trong hệ trục tọa độ \[Oxyz\] với đơn vị là mét với mặt phẳng \[(R):z + 1 = 0\] là mặt đất (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2026/01/blobid14-1767803099.png)
Xét phép quay tâm \(A\) góc quay \( - 60^\circ \) biến điểm \(M \in a\) thành \(M' \in b\).
Đặt \(\widehat {MAH} = \alpha \Rightarrow \widehat {M'AK} = 120^\circ - \widehat {MAH} - \widehat {MAM'} = 60^\circ - \alpha \)
Xét \(\Delta MAH\) vuông tại \(H\), có: \(MA = \frac{{AH}}{{\cos \alpha }} = \frac{2}{{\cos \alpha }}\).
Xét \(\Delta M'AK\)vuông tại \(K\), có: \(AM' = \frac{{AK}}{{\cos \left( {60^\circ - \alpha } \right)}} = \frac{1}{{\cos \left( {60^\circ - \alpha } \right)}}\).
Mà \(AM = AM' \Leftrightarrow \cos \alpha = 2\cos \left( {60^\circ - \alpha } \right)\)
\[\begin{array}{l} \Leftrightarrow \cos \alpha = 2\left( {\cos 60^\circ .\cos \alpha + \sin 60.\sin \alpha } \right)\\ \Leftrightarrow \sqrt 3 \sin \alpha = 0\\ \Rightarrow \alpha = 0\end{array}\]
Vậy \(M \equiv H\). Vậy \(\Delta ABC\) đều \( \Rightarrow B \equiv H\) và thực hiện phép quay tâm \(A\), góc quay \( - 60^\circ \) biến điểm \(H\) thành điểm \(C.\)
![Mái nhà tranh của ông F được đặt vào trong hệ trục tọa độ \[Oxyz\] với đơn vị là mét với mặt phẳng \[(R):z + 1 = 0\] là mặt đất (ảnh 3)](https://video.vietjack.com/upload2/quiz_source1/2026/01/blobid15-1767803110.png)
Suy ra \(C\) thuộc mp\((\beta )\) là mặt phẳng trung trực của \(AH\) hay mặt phẳng cách đều \(A\) và \((P).\)
Gọi \(d\) là đường thẳng qua \(A\) và vuông góc với \((P).\) Khi đó: \(d:\left\{ \begin{array}{l}x = 1 + t\\y = - 1 + t\\z = 1\end{array} \right.\)
\(B = d \cap (P) \Rightarrow \left\{ \begin{array}{l}x + y - 2\sqrt 2 = 0\\x = 1 + t\\y = - 1 + t\\z = 1\end{array} \right. \Rightarrow B(1 + \sqrt 2 ;\sqrt 2 - 1;1).\)
Gọi \(M\) là trung điểm
Tọa độ của \(C\) là nghiệm của hệ phương trình là phương trình của 3 mặt phẳng \((Q),(\alpha ),(\beta ).\)
\(\left\{ \begin{array}{l}x - z + \sqrt 2 = 0\\x - y + z - 3 = 0\\x + y - \sqrt 2 = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 1\\y = \sqrt 2 - 1\\z = \sqrt 2 + 1\end{array} \right. \Rightarrow C\left( {1;\sqrt 2 - 1;\sqrt 2 + 1} \right).\)
Vậy chiều cao mét của khoen móc \[C\] so với mặt đất là
\(h = d(C;(R)) = \frac{{|{z_C} + 1|}}{1} = \left| {\sqrt 2 + 1 + 1} \right| = 2 + \sqrt 2 \approx 3,4{\rm{ m}}{\rm{.}}\)
Câu 2
a) [NB] Thầy quản nhiệm muốn chia lớp ra thành 4 tổ, mỗi tổ có 10 bạn thì có \(C_{40}^{10}.C_{30}^{10}.C_{20}^{10}\) cách.
b) [TH] Xác suất để thầy quản nhiệm chia lớp ra thành 4 tổ, mỗi tổ có 10 bạn sao cho số lượng nam và nữ của mỗi tổ bằng nhau là \(0,03\). (Làm tròn đến hàng phần trăm)
c) [TH] Thầy quản nhiệm có thể chia lớp ra thành 4 tổ, mỗi tổ có 10 bạn sao cho số lượng các bạn nữ của các tổ lập thành một cấp số cộng và số lượng các bạn nam của mỗi tổ cũng vậy.
Lời giải
a) [NB] Thầy quản nhiệm muốn chia lớp ra thành 4 tổ, mỗi tổ có 10 bạn thì có \(C_{40}^{10}.C_{30}^{10}.C_{20}^{10}\) cách.
Số cách chia lớp thành 4 tổ, mỗi tổ 10 bạn là \(C_{40}^{10}.C_{30}^{10}.C_{20}^{10}.C_{10}^{10} = C_{40}^{10}.C_{30}^{10}.C_{20}^{10}\) (cách)
Vậy a) đúng.
b) [TH] Xác suất để thầy quản nhiệm chia lớp ra thành 4 tổ, mỗi tổ có 10 bạn sao cho số lượng nam và nữ của mỗi tổ bằng nhau là \(0,03\). (Làm tròn đến hàng phần trăm)
Mỗi tổ 10 bạn sao cho số lượng nam và nữ của mỗi tổ bằng nhau thì mỗi tổ có 5 nam và 5 nữ. Xác suất chia như vậy là
\(\frac{{C_{20}^5.C_{20}^5.C_{15}^5.C_{15}^5.C_{10}^5.C_{10}^5}}{{C_{40}^{10}.C_{30}^{10}.C_{20}^{10}}} \approx 0,03\).
Vậy b) đúng.
c) [TH] Thầy quản nhiệm có thể chia lớp ra thành 4 tổ, mỗi tổ có 10 bạn sao cho số lượng các bạn nữ của các tổ lập thành một cấp số cộng và số lượng các bạn nam của mỗi tổ cũng vậy.
Mỗi tổ có 5 nam và 5 nữ hoặc 4 tổ có số lượng nữ lần lượt là 2, 4, 6, 8 và nam lần lượt là 8, 6, 4, 2 thì thỏa mãn yêu cầu bài toán.
Vậy c) đúng.
d) [VD,VDC] Nghe lời thầy F có am hiểu về phong thủy, để cả lớp đạt NV1 trong kì thi quốc gia sắp tới thầy quản nhiệm chia lớp ra thành 4 tổ, mỗi tổ có 10 bạn sao cho tổ nào cũng có nam lẫn nữ và sự chênh lệch giữa số lượng nam và nữ trong tổ nhiều hơn 3 bạn. Nếu gọi \({k_1},{k_2},{k_3},{k_4}\)lần lượt là hiệu số giữa số lượng nam và nữ của tổ 1, 2, 3 và 4 thì \(\left\{ {{k_1},{k_2},{k_3},{k_4}} \right\}\) lập thành một cấp số nhân với công bội \(q \ne 1\). Xác suất để thầy quản nhiệm chia như vậy lớn hơn \(0,0015\).
Gọi \(a\) là số nam của một tổ, suy ra số nữ một tổ là \(10 - a\).
Vì sự chênh lệch giữa số lượng nam và nữ trong tổ nhiều hơn 3 bạn nên \(\left| {10 - a - a} \right| > 3\)
Suy ra \(\left[ \begin{array}{l}10 - 2a > 3\\10 - 2a < - 3\end{array} \right. \Rightarrow \left[ \begin{array}{l}a < \frac{7}{2}\\a > \frac{{13}}{2}\end{array} \right.\). Mà \(a\) nguyên nên \(a \in \left\{ {1\,;\,2\,;\,3\,;\,7\,;\,8\,;\,9} \right\}\).
Do đó tương ứng \({k_i} \in \left\{ {8\,;\,6\,;\,4\,;\, - 4\,;\, - 6\,;\, - 8} \right\},\,i = 1,\,2,\,3,\,4\).
Lại có \(\left\{ {{k_1},{k_2},{k_3},{k_4}} \right\}\) lập thành một cấp số nhân với công bội \(q \ne 1\) nên \({k_i},\,i = 1,\,2,\,3,\,4\), đôi một khác nhau và \(k_i^2 = {k_{i - 1}}.{k_{i + 1}}\) nên bộ số \(\left\{ {{k_1},{k_2},{k_3},{k_4}} \right\}\) nhận các bộ số sau \(\left\{ {6, - 6,6, - 6} \right\}\), \(\left\{ {4, - 4,4, - 4} \right\}\), \(\left\{ {8, - 8,8, - 8} \right\}\). Như vậy thầy quản nhiệm có thể chia 4 tổ sao cho 2 tổ có 2 nam, 8 nữ và 2 tổ có 8 nam, 2 nữ hoặc 2 tổ có 3 nam, 7 nữ và 2 tổ 7 nam, 3 nữ hoặc 2 tổ có 1 nam, 9 nữ và 2 tổ 1 nữ, 9 nam. Xác suất chia như vậy là
\[\frac{{C_{20}^2.C_{20}^8.C_{18}^8.C_{12}^2.C_{10}^2.C_{10}^8 + C_{20}^3.C_{20}^7.C_{17}^7.C_{13}^3.C_{10}^3.C_{10}^3 + C_{20}^1.C_{20}^9.C_{19}^9.C_{11}^1.C_{10}^1.C_{10}^9}}{{C_{40}^{10}.C_{30}^{10}.C_{20}^{10}}} \approx 0,001534 > 0,0015\].
Vậy d) đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
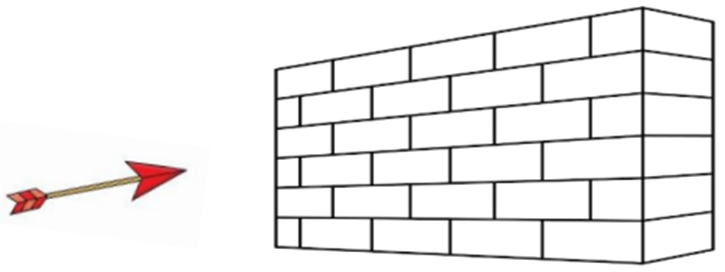
a) Quả táo cách bức tường \(4m\).
b) Một người bắn một mũi tên với đầu mũi tên là \(B\left( {2; - 1;4} \right)\) theo hướng \(\vec a = \left( {2;4;0} \right)\) thì mũi tên bay xuyên qua trái táo.
c) Mũi tên cắm vào bức tường tại điểm \(C\left( {5;5;4} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Mái nhà tranh của ông F được đặt vào trong hệ trục tọa độ \[Oxyz\] với đơn vị là mét với mặt phẳng \[(R):z + 1 = 0\] là mặt đất (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/blobid13-1767803090.png)