Tìm công sai \[d\] của cấp số cộng \[\left( {{u_n}} \right),n \in {N^*}\] có \[{u_1} = 1;{u_4} = 13\] có tập nghiệm là
Quảng cáo
Trả lời:
Chọn D
Ta có \[\left\{ \begin{array}{l}{u_1} = 1\\{u_4} = 13\end{array} \right. \Leftrightarrow {u_4} = {u_1} + 3d \Leftrightarrow d = \frac{{{u_4} - {u_1}}}{3} = 4\].
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Có \[n \in N\].
Gọi \[a,b,c\] lần lượt là số ghế của Khoa, Thảo, Khôi. Do \[a,b,c\] là cấp số cộng nên \[a + c = 2b\].
Chứng tỏ \[a,c\] cùng chẵn hoặc cùng lẻ.
Gọi \[A\] là tập hợp các ghế số chẵn, \[B\] là tập hợp các ghế số lẻ.
Với hai phần tử \[a,c\] thuộc \[A\] hoặc \[B\] thì hiển nhiên tồn tại cấp số cộng \[a,b,c\].
Trường hợp \[n\] chẵn.
Khi đó, \[A\] có \[\frac{n}{2}\] phần tử và \[B\] có \[\frac{n}{2}\] phần tử.
Có \[C_{\frac{n}{2}}^2 = \frac{{\left( {\frac{n}{2}} \right)!}}{{2!.\left( {\frac{n}{2} - 2} \right)!}} = \frac{1}{2}.\left( {\frac{n}{2} - 1} \right)\left( {\frac{n}{2}} \right) = \frac{1}{8}.\left( {n - 2} \right).n\], nên số cấp số cộng là \[2.C_{\frac{n}{2}}^2 = \frac{1}{4}.\left( {n - 2} \right).n\]
và số kết quả thuận lợi là \[\frac{1}{4}.\left( {n - 2} \right).n.2.\left( {n - 3} \right)! = \frac{1}{2}.\left( {n - 2} \right).n.\left( {n - 3} \right)!\] (do mỗi bộ \[\left( {a;b;c} \right)\] có \[2\] cấp số cộng và ba bạn Khoa, Thảo, Khôi chỉ ngồi vào ba ghế có số ghế tạo thành cấp số cộng chứ không thay đổi vị trí).
Theo đề, có phương trình. \[\frac{{\frac{1}{2}.\left( {n - 2} \right).n.\left( {n - 3} \right)!}}{{n!}} = \frac{{13}}{{675}} \Leftrightarrow \frac{1}{{2\left( {n - 1} \right)}} = \frac{{13}}{{675}} \Leftrightarrow n = \frac{{701}}{{26}}\] (loại).
Trường hợp \[n\] lẻ.
Khi đó, \[A\] có \[\frac{{n - 1}}{2}\] phần tử và \[B\] có \[\frac{{n + 1}}{2}\] phần tử.
Có \[C_{\frac{{n - 1}}{2}}^2 = \frac{{\left( {\frac{{n - 1}}{2}} \right)!}}{{2!.\left( {\frac{{n - 1}}{2} - 2} \right)!}} = \frac{1}{2}.\left( {\frac{{n - 1}}{2} - 1} \right).\left( {\frac{{n - 1}}{2}} \right) = \frac{1}{8}.\left( {n - 3} \right).\left( {n - 1} \right)\]
và \[C_{\frac{{n + 1}}{2}}^2 = \frac{{\left( {\frac{{n + 1}}{2}} \right)!}}{{2!.\left( {\frac{{n + 1}}{2} - 2} \right)!}} = \frac{1}{2}.\left( {\frac{{n + 1}}{2} - 1} \right)\left( {\frac{{n + 1}}{2}} \right) = \frac{1}{8}.\left( {n - 1} \right).\left( {n + 1} \right)\],
nên số cấp số cộng là \[C_{\frac{{n - 1}}{2}}^2 + C_{\frac{{n + 1}}{2}}^2 = \frac{1}{8}\left( {n - 1} \right)\left( {2n - 2} \right) = \frac{1}{4}{\left( {n - 1} \right)^2}\]
và số kết quả có thể là \[\frac{1}{4}{\left( {n - 1} \right)^2}.2.\left( {n - 3} \right)! = \frac{1}{2}{\left( {n - 1} \right)^2}.\left( {n - 3} \right)!\](do mỗi bộ \[\left( {a;b;c} \right)\] có \[2\] cấp số cộng và ba bạn Khoa, Thảo, Khôi chỉ ngồi vào ba ghế có số ghế tạo thành cấp số cộng chứ không thay đổi vị trí).
Theo đề, có phương trình.
\[\frac{{\frac{1}{2}.{{\left( {n - 1} \right)}^2}.\left( {n - 3} \right)!}}{{n!}} = \frac{{13}}{{675}} \Leftrightarrow \frac{{n - 1}}{{2n\left( {n - 2} \right)}} = \frac{{13}}{{675}} \Leftrightarrow 26{n^2} - 727n + 675 = 0 \Leftrightarrow \left[ \begin{array}{l}n = 27\;\left( n \right)\\n = \frac{{25}}{{26}}\;\left( l \right)\end{array} \right.\]
Câu 2
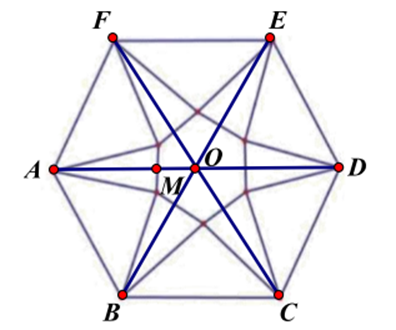
a) [NB] Tam giác OAB đều có cạnh bằng 4 cm.
b) [TH] Cạnh đáy của khối chóp lục giác đều bằng \(\frac{{x\sqrt 3 }}{6}\) (cm).
c) [TH] Đường cao của khối chóp lục giác đều bằng \(\sqrt {16 - 8x} \,\,\)(cm).
Lời giải
a) Đúng
b) Sai
Vì OM là độ dài đường cao của tam giác cạnh bằng cạnh đáy của khối chóp lục giác đều nên cạnh đáy của khối chóp lục giác đều bằng \(\frac{2}{{\sqrt 3 }}x = \frac{{2\sqrt 3 }}{3}x\).
c) Đúng
Ta có. \(AM = 4 - x\)nên chiều cao khối chóp lục giác đều là \(\sqrt {{{\left( {4 - x} \right)}^2} - {x^2}} = \sqrt {16 - 8x} \).
d) Sai
Thể tích khối chóp lục giác đều là
\(V\) lớn nhất \( \Leftrightarrow 64{x^3} - 40{x^4} = 0 \Rightarrow x = \frac{8}{5}.\)
Khi đó. Thể tích lớn nhất của khối chóp lục giác đều bằng .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
a) [NB] Xác suất An không câu được cá bằng \[0,4\]
b) [TH] Xác suất có đúng 1 người câu được cá bằng \[0,34\]
c) [TH] Xác suất để cả 2 người đều không câu được cá bằng \[0,3\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

![[VD] Hãng Xtul Air – Công ty chuyên về các chuyến bay thuê chuyến vừa có hoạt động thâm nhập thị trường Việt Nam (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/blobid12-1767807675.png)
![An và Bình rủ nhau đi câu cá vào ngày nghỉ cuối tuần. Xác suất câu được cá của An là \[0,6\]. Xác suất câu được cá của Bình là \[0,3\]. Khi đó ta có (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/blobid9-1767807523.png)