Trong cơ thể người, hemoglobin (Hb) kết hợp oxygen phản ứng của người được biểu diễn đơn giản như sau: $\text{Hb}+{{\text{O}}_{2}}\text{Hb}{{\text{O}}_{2}}$
Ở phổi, nồng độ oxygen lớn nên cân bằng trên chuyển dịch sang phải, hemoglobin kết hợp với oxygen. Khi đến các mô, nồng độ oxygen thấp, cân bằng trên chuyển dịch sang trái, giải phóng oxygen. Nếu thiếu oxygen ở não, con người có thể bị đau đầu, chóng mặt.
Vận dụng nguyên lý chuyển dịch cân bằng Le Chatelier, biện pháp nào sau đây giúp oxygen lên não nhiều hơn?
Trong cơ thể người, hemoglobin (Hb) kết hợp oxygen phản ứng của người được biểu diễn đơn giản như sau: $\text{Hb}+{{\text{O}}_{2}}\text{Hb}{{\text{O}}_{2}}$
Ở phổi, nồng độ oxygen lớn nên cân bằng trên chuyển dịch sang phải, hemoglobin kết hợp với oxygen. Khi đến các mô, nồng độ oxygen thấp, cân bằng trên chuyển dịch sang trái, giải phóng oxygen. Nếu thiếu oxygen ở não, con người có thể bị đau đầu, chóng mặt.
Vận dụng nguyên lý chuyển dịch cân bằng Le Chatelier, biện pháp nào sau đây giúp oxygen lên não nhiều hơn?

Quảng cáo
Trả lời:
Để oxygen lên não nhiều hơn thì hàm lượng oxygen hít vào phổi cũng phải nhiều hơn ![]() cần hít thở sâu, trồng nhiều cây xanh, bảo vệ không khí không bị ô nhiễm để không khí trong lành, nồng độ oxygen trong không khí ổn định.
cần hít thở sâu, trồng nhiều cây xanh, bảo vệ không khí không bị ô nhiễm để không khí trong lành, nồng độ oxygen trong không khí ổn định.
Chọn A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Tại \({t_0} = 70\) ta có: \(T\left( {70} \right) = 300\).
\(\mathop {\lim }\limits_{t \to {{70}^ - }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{70}^ - }} \left( {20 + 4t} \right) = 300\); \(\mathop {\lim }\limits_{t \to {{70}^ + }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{70}^ + }} \left( {a - 2t} \right) = a - 140\).
Hàm số liên tục trên tập xác định khi: \(\mathop {\lim }\limits_{t \to {{70}^ - }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{70}^ + }} T\left( t \right) = T\left( {70} \right)\)
\( \Leftrightarrow a - 140 = 300\)\( \Leftrightarrow a = 440\). Vậy giá trị của \(a = 440^\circ {\rm{C}}\). Chọn A.
Câu 2
Lời giải
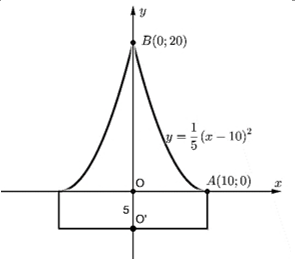
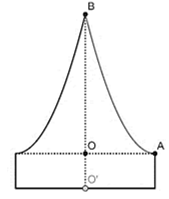
Chọn hệ trục tọa độ như hình vẽ bên.
Ta gọi thể tích của chiếc mũ là \(V\).
Thể tích của khối trụ có bán kính đáy bằng \(OA = 10\)cm và đường cao \(OO' = 5\)cm là \({V_1}\).
Thể tích của vật thể tròn xoay khi quay hình phẳng giới hạn bởi đường cong \(AB\) và hai trục tọa độ quanh trục \(Oy\) là \({V_2}\). Khi đó, ta có \(V = {V_1} + {V_2}\).
Ta có \({V_1} = 5 \cdot {10^2}\pi = 500\pi \) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Do parabol có đỉnh \(A\) nên nó có phương trình dạng \(\left( P \right):y = a{\left( {x - 10} \right)^2}\). Vì \(\left( P \right)\) qua điểm \(B\left( {0;20} \right)\) nên \(a = \frac{1}{5}\). Do đó, \(\left( P \right):y = \frac{1}{5}{\left( {x - 10} \right)^2}\). Từ đó suy ra \(x = 10 - \sqrt {5y} \) (do \(x < 10\)).
Suy ra \({V_2} = \pi \int\limits_0^{20} {{{\left( {10 - \sqrt {5y} } \right)}^2}{\rm{dy}}} = \pi \left( {3000 - \frac{{8000}}{3}} \right) = \frac{{1000}}{3}\pi \) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Do đó \(V = {V_1} + {V_2} = \frac{{1000}}{3}\pi + 500\pi = \frac{{2500}}{3}\pi \) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\). Chọn B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
 .
.