Điểm kiểm tra môn Toán của một số học sinh được thống kê ở bảng
A. Mốt của mẫu số liệu trên là 10.
Đúng
Sai
B. Khoảng biến thiên của mẫu số liệu trên là 7.
Đúng
Sai
C. Mẫu số liệu trên có 2 giá trị ngoại lệ.
Đúng
Sai
D. Sau khi bỏ đi các giá trị ngoại lệ, điểm thi trung bình của mẫu số liệu trên là \(7,8\) (làm tròn kết quả đến hàng phần chục).
Đúng
Sai
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Sắp xếp lại mẫu số liệu trên theo thứ tự không giảm dưới dạng bảng ta được
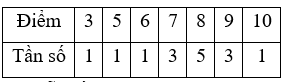
Điểm 8 có tần số lớn nhất nên mốt của mẫu số liệu là 8.
b) Khoảng biến thiên \(R = 10 - 3 = 7\).
c) Mẫu số liệu có 15 giá trị nên \({Q_1} = 7;{Q_2} = 9\).
Do đó \({\Delta _Q} = 9 - 7 = 2\).
Có \({Q_1} - 1,5{\Delta _Q} = 7 - 1,5 \cdot 2 = 4;{Q_3} + 1,5{\Delta _Q} = 9 + 1,5 \cdot 2 = 12\).
Do đó 3 là giá trị ngoại lệ của mẫu số liệu. Vậy mẫu số liệu có 1 giá trị ngoại lệ.
d) Điểm thi trung bình khi bỏ đi giá trị ngoại lệ là \(\overline x = \frac{{5 + 6 + 7 \cdot 3 + 8 \cdot 5 + 9 \cdot 3 + 10}}{{14}} \approx 7,8\).
Đáp án: a) Sai; b) Đúng; c) Sai; d) Đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Giá trị trung bình là \(\overline x = \frac{{15 + 20 + 1 + 2 + 4 + 3 + 7 + 5}}{8} = 7,125\).
Phương sai \({s^2} = \frac{1}{8}\left[ \begin{array}{l}{\left( {15 - 7,125} \right)^2} + {\left( {20 - 7,125} \right)^2} + {\left( {1 - 7,125} \right)^2} + {\left( {2 - 7,125} \right)^2}\\ + {\left( {4 - 7,125} \right)^2} + {\left( {3 - 7,125} \right)^2} + {\left( {7 - 7,125} \right)^2} + {\left( {5 - 7,125} \right)^2}\end{array} \right] \approx 40,4\).
Trả lời: 40,4.
Lời giải
Khoảng biến thiên \(R = 172 - 159 = 13\).
Trả lời: 13.
Câu 3
A. \({Q_3} - {Q_1}\).
B. \({Q_2} - {Q_1}\).
C. \({Q_3} - {Q_2}\).
D. \(\frac{{{Q_1} + {Q_3}}}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(64\).
B. \(14\).
C. \(202,5\).
D. \(100,875\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Phương sai \({s^2} = 17,61\).
Đúng
Sai
B. Khoảng tứ phân vị là \({\Delta _Q} = 7\).
Đúng
Sai
C. Số trung vị là \({M_e} = 164\).
Đúng
Sai
D. Khoảng biến thiên là \(R = 12\).
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập