Cho ba số đôi một khác nhau và khác \(0.\)
Biết \(\frac{a}{{b - c}} + \frac{b}{{c - a}} + \frac{c}{{a - b}} = 0,\) tính giá trị của biểu thức \(\frac{a}{{{{\left( {b - c} \right)}^2}}} + \frac{b}{{{{\left( {c - a} \right)}^2}}} + \frac{c}{{{{\left( {a - b} \right)}^2}}}.\)
Cho ba số đôi một khác nhau và khác \(0.\)
Biết \(\frac{a}{{b - c}} + \frac{b}{{c - a}} + \frac{c}{{a - b}} = 0,\) tính giá trị của biểu thức \(\frac{a}{{{{\left( {b - c} \right)}^2}}} + \frac{b}{{{{\left( {c - a} \right)}^2}}} + \frac{c}{{{{\left( {a - b} \right)}^2}}}.\)
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Với \(a \ne b \ne c \ne 0,\) từ \(\frac{a}{{b - c}} + \frac{b}{{c - a}} + \frac{c}{{a - b}} = 0,\) suy ra:
\(\frac{a}{{b - c}} = \frac{b}{{a - c}} + \frac{c}{{b - a}} = \frac{{b\left( {b - a} \right)}}{{\left( {a - c} \right)\left( {b - a} \right)}} + \frac{{c\left( {a - c} \right)}}{{\left( {a - c} \right)\left( {b - a} \right)}} = \frac{{{b^2} - ab + ac - {c^2}}}{{\left( {a - c} \right)\left( {b - a} \right)}}.\)
Nhân hai vế với \(\frac{1}{{b - c}}\) ta được:
\(\frac{a}{{{{\left( {b - c} \right)}^2}}} = \frac{{{b^2} - ab + ac - {c^2}}}{{\left( {a - c} \right)\left( {b - a} \right)\left( {b - c} \right)}} = \frac{{{b^2} - ab + ac - {c^2}}}{{\left( {a - b} \right)\left( {b - c} \right)\left( {c - a} \right)}}.\)
Tương tư, ta có: \(\frac{b}{{{{\left( {c - a} \right)}^2}}} = \frac{{{c^2} - bc + ab - {a^2}}}{{\left( {a - b} \right)\left( {b - c} \right)\left( {c - a} \right)}};\,\,\frac{c}{{{{\left( {a - b} \right)}^2}}} = \frac{{{a^2} - ca + bc - {b^2}}}{{\left( {a - b} \right)\left( {b - c} \right)\left( {c - a} \right)}}.\)
Cộng vế theo vế ba đẳng thức trên ta được:
\(\frac{a}{{{{\left( {b - c} \right)}^2}}} + \frac{b}{{{{\left( {c - a} \right)}^2}}} + \frac{c}{{{{\left( {a - b} \right)}^2}}}\)
\( = \frac{{{b^2} - ab + ac - {c^2}}}{{\left( {a - b} \right)\left( {b - c} \right)\left( {c - a} \right)}} + \frac{{{c^2} - bc + ab - {a^2}}}{{\left( {a - b} \right)\left( {b - c} \right)\left( {c - a} \right)}} + \frac{{{a^2} - ca + bc - {b^2}}}{{\left( {a - b} \right)\left( {b - c} \right)\left( {c - a} \right)}}\)
\( = \frac{0}{{\left( {a - b} \right)\left( {b - c} \right)\left( {c - a} \right)}} = 0.\)
Vậy \(\frac{a}{{{{\left( {b - c} \right)}^2}}} + \frac{b}{{{{\left( {c - a} \right)}^2}}} + \frac{c}{{{{\left( {a - b} \right)}^2}}} = 0.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
a) \[x - 3\left( {2 - x} \right) = 2x - 4\]
\[x - 6 + 3x = 2x - 4\]
\[x + 3x - 2x = 6 - 4\]
\[2x = 2\]
\[x = 1\]
Vậy phương trình đã cho có nghiệm \(x = 1.\)b) \[\frac{1}{3}\left( {x - 1} \right) + 4 = \frac{1}{2}\left( {x + 5} \right)\]
\[2\left( {x - 1} \right) + 24 = 3\left( {x + 5} \right)\]
\[2x - 2 + 24 = 3x + 15\]
\(2x - 3x = 15 + 2 - 24\)
\[ - x = - 7\]
\[x = 7\]
Vậy phương trình đã cho có nghiệm \(x = 7.\)
Lời giải
Hướng dẫn giải
1) Hình vẽ bên mô tả bậc tam cấp.
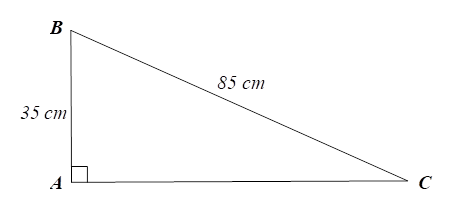
Xét \(\Delta ABC\) vuông tại \(A,\) theo định lí Pythagore ta có: \(B{C^2} = A{B^2} + A{C^2}\)
Suy ra \(A{C^2} = B{C^2} - A{B^2} = {85^2} - {35^2} = 6\,\,000.\)
Do đó \(AC = \sqrt {6\,\,000} \approx 77,46{\rm{\;cm}} < 80{\rm{\;cm}}.\)Vậy bậc tam cấp nhà bạn Thanh phù hơp với quy định của khu phố.
2)
a) Do \(ABCD\) là hình bình hành nên \(AB\,{\rm{//}}\,CD\) và \(AD\,{\rm{//}}\,BC.\)
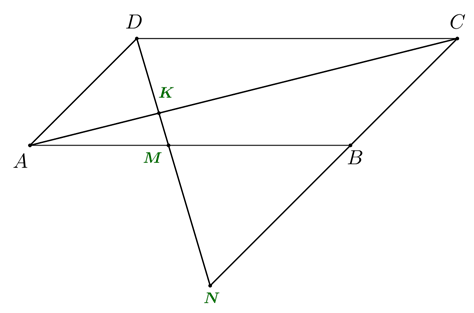
Xét \(\Delta ADK\) có \(AD\,{\rm{//}}\,CN\) (do \(AD\,{\rm{//}}\,BC)\) nên (g.g).
b) Xét \(\Delta KAM\) có \(AM\,{\rm{//}}\,CD\) (do \(AB\,{\rm{//}}\,CD)\) nên (g.g).
Mà (câu a) nên \(\frac{{KD}}{{KN}} = \frac{{AK}}{{CK}}\) (tỉ số cạnh tương ứng).
Suy ra \(\frac{{KD}}{{KN}} = \frac{{KM}}{{KD}}\) nên \(K{D^2} = KM \cdot KN.\)
c) Do nên \(\frac{{AK}}{{CK}} = \frac{{AD}}{{CN}}\) (tỉ số cạnh tương ứng).
Do nên \(\frac{{AK}}{{CK}} = \frac{{AM}}{{CD}}\) (tỉ số cạnh tương ứng).
Suy ra \(\frac{{AD}}{{CN}} = \frac{{AM}}{{CD}}\) hay \(\frac{9}{{CN}} = \frac{6}{{10}},\) do đó \(CN = \frac{{9 \cdot 10}}{6} = 15\) (cm).
Câu 3
A. \(\frac{1}{2}.\)
B. \(\frac{1}{{2y}}.\)
C. \(\frac{{2x}}{{{y^2}}}.\)
D. \(\frac{{2{x^2}}}{{{y^2}}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\frac{{{x^2} - 1}}{{2x - 1}}.\)
B. \(\frac{{2x - 1}}{{{x^2} + 1}}.\)
C. \(\frac{{2x - 1}}{{{x^2} - 1}}.\)
D. \(\frac{{{x^2} - 1}}{{2x + 1}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(2x - {2^2} = 0.\)
B. \({x^2} = 1.\)
C. \(x - y = 0.\)
D. \(1 - \frac{1}{x} = 0.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(8{\rm{\;cm}}.\)
B. \(9{\rm{\;cm}}.\)
C. \(10{\rm{\;cm}}.\)
D. \(12{\rm{\;cm}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập