Một hộp chứa các quả bóng giống nhau có các màu xanh dương, cam và vàng. Trong 30 lần lấy bóng liên tiếp, quả bóng cam xuất hiện 10 lần và quả bóng vàng xuất hiện 8 lần. Xác suất thực nghiệm của biến cố “Quả bóng lấy ra là quả bóng màu xanh dương” là
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: D
Xác suất thực nghiệm của biến cố “Quả bóng lấy ra là quả bóng màu xanh dương” là
\(\frac{{30 - 10 - 8}}{{30}} = \frac{{12}}{{30}} = \frac{2}{5}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
a) Trong các mặt hàng trên, sản phẩm được giảm giá nhiều nhất là áo sơ mi giảm \(35\% ,\) sản phẩm được giảm giá ít nhất là quần Jean giảm \(10\% .\)
b) An nên dùng biểu đồ cột để biểu diễn.
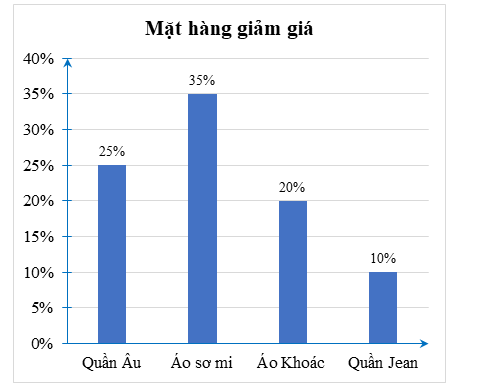
c) Áo sơ mi giảm \(35\% ,\) giá sau giảm là \(325\,\,000\) đồng. Do đó mỗi chiếc áo sơ mi nguyên giá sẽ là \(325\,\,000:65\% = 500\,\,000\) (đồng).
Giá một chiếc quần Âu sau giảm là \(\frac{{1\,\,850\,\,000 - 325\,\,000 \cdot 2}}{4} = 300\,\,000\) (đồng).
Quần âu giảm giá \(25\% ,\) do đó mỗi chiếc quần âu nguyên giá sẽ là
\(300\,\,000:75\% = 400\,\,000\) (đồng).
Câu 2
Lời giải
Hướng dẫn giải
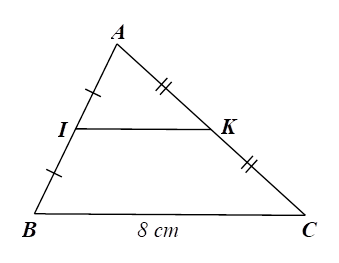
Đáp án đúng là: A
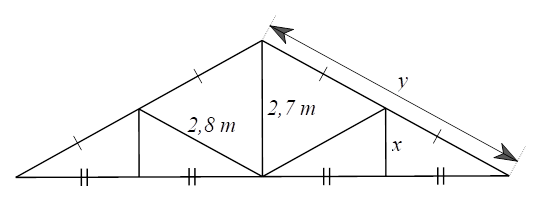
Xét \(\Delta ABC\) có \(I,\,\,K\) lần lượt là trung điểm của \(AB\) và \(AC\) nên \(IK\) là đường trung bình của tam giác, do đó \(\frac{{IK}}{{BC}} = \frac{1}{2},\) suy ra \(IK = \frac{{BC}}{2} = \frac{8}{2} = 4{\rm{\;cm}}.\)Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.