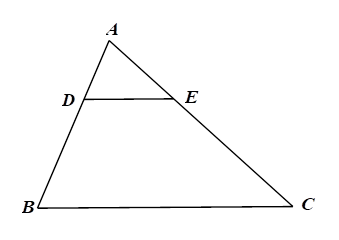
1) Cho tam giác \(ABC\) có \(BC = 15{\rm{\;cm}},\,\,CA = 18{\rm{\;cm}}\) và \(AB = 12{\rm{\;cm}}.\) Gọi \(I\) và \(G\) lần lượt là tâm đường tròn nội tiếp và trọng tâm \(\Delta ABC.\)
a) Tính độ dài các đoạn thẳng \(CD\) và \(BD.\)
b) Chứng minh \(IG\,{\rm{//}}\,BC.\)
c) Tính độ dài đoạn thẳng \(IG.\)
2) Vì kèo mái tôn là một trong những bộ phận không thể thiếu trong cấu tạo mái nhà lợp tôn. Nó giúp chống đỡ và giảm trọng lực của những ảnh hưởng từ các yếu tố bên ngoài tác động vào (Hình a).
Hình a
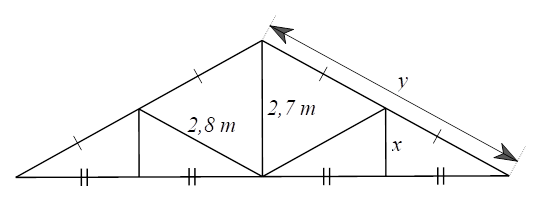
Hình b
Một vì kèo mái tôn được vẽ lại như Hình b. Tính độ dài \(x\) của cây chống đứng bên và độ dài \(y\) của cánh kèo.
1) Cho tam giác \(ABC\) có \(BC = 15{\rm{\;cm}},\,\,CA = 18{\rm{\;cm}}\) và \(AB = 12{\rm{\;cm}}.\) Gọi \(I\) và \(G\) lần lượt là tâm đường tròn nội tiếp và trọng tâm \(\Delta ABC.\)
a) Tính độ dài các đoạn thẳng \(CD\) và \(BD.\)
b) Chứng minh \(IG\,{\rm{//}}\,BC.\)
c) Tính độ dài đoạn thẳng \(IG.\)
2) Vì kèo mái tôn là một trong những bộ phận không thể thiếu trong cấu tạo mái nhà lợp tôn. Nó giúp chống đỡ và giảm trọng lực của những ảnh hưởng từ các yếu tố bên ngoài tác động vào (Hình a).
|
Hình a |
Hình b |
Một vì kèo mái tôn được vẽ lại như Hình b. Tính độ dài \(x\) của cây chống đứng bên và độ dài \(y\) của cánh kèo.
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
1)
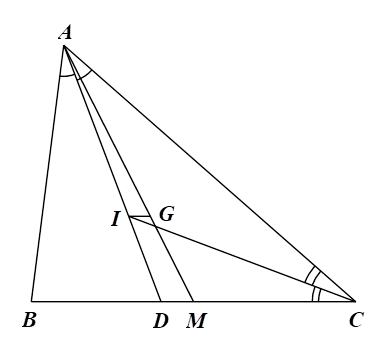
a) Gọi \(AD\) là đường phân giác góc \(BAC\) \(\left( {D \in BC} \right).\)
Xét \(\Delta ABC\) có \(AD\) là đường phân giác của \(\widehat {BAC}\) nên \[\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}},\] hay \[\frac{{DC}}{{AC}} = \frac{{DB}}{{AB}}.\]
Theo tính chất dãy tỉ số bằng nhau ta có:
\[\frac{{DC}}{{AC}} = \frac{{DB}}{{AB}} = \frac{{DC + DB}}{{AC + AB}} = \frac{{BC}}{{AC + AB}} = \frac{{15}}{{18 + 12}} = \frac{1}{2}.\]Suy ra \(CD = \frac{1}{2}AC = \frac{1}{2} \cdot 18 = 9{\rm{\;cm}}\) và \(BD = \frac{1}{2}AB = \frac{1}{2} \cdot 12 = 6{\rm{\;cm}}.\)
b) Xét \(\Delta ACD,\) có \(CI\) là đường phân giác của \(\widehat {ACD}\) nên \(\frac{{AI}}{{DI}} = \frac{{AC}}{{CD}} = \frac{{18}}{9} = 2.\)
Mặt khác, do \(G\) là trọng tâm của \(\Delta ABC\) nên \(\frac{{AG}}{{GM}} = 2.\)
Do đó \(\frac{{AI}}{{ID}} = \frac{{AG}}{{GM}} = 2,\) theo định lí Thalès đảo ta có \(IG\,{\rm{//}}\,BC.\)
b) Gọi \(M\) là trung điểm của \(BC.\) Khi đó \[MB = MC = \frac{1}{2}BC = \frac{1}{2} \cdot 15 = 7,5{\rm{\;cm}}.\]
Suy ra \(DM = BM - BD = 7,5 - 6 = 1,5{\rm{\;cm}}.\)
Xét \(\Delta ADM\) có \(IG\,{\rm{//}}\,BC,\) theo hệ quả định lí Thalès ta có \(\frac{{IG}}{{DM}} = \frac{{AG}}{{AM}} = \frac{2}{3}.\)
Suy ra \(IG = \frac{2}{3}DM = \frac{2}{3} \cdot 1,5 = 1{\rm{\;cm}}.\)
2)
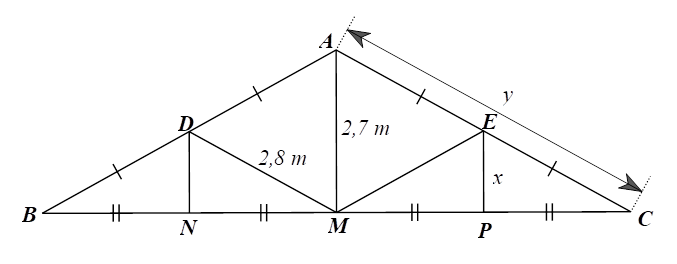
Đặt các điểm \[A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D,{\rm{ }}E,{\rm{ }}M,{\rm{ }}N,{\rm{ }}P\] như hình vẽ trên.
⦁ Xét \(\Delta AMC\) có \(E,\,\,P\) lần lượt là trung điểm của \(AC,\,\,MC\) (do \(EA = EC,PM = PC)\) nên \(EP\) là đường trung bình của \(\Delta AMC.\)
Do đó \(EP = \frac{1}{2}AM = \frac{1}{2} \cdot 2,7 = 1,35{\rm{\;}}\left( {\rm{m}} \right)\) (tính chất đường trung bình của tam giác).
Hay \(x = 1,35{\rm{\;}}\left( {\rm{m}} \right){\rm{.}}\)
⦁ Ta có \(MB = MN + NB\) và \(MC = MP + PC\)
Mà \(MN = NB = MP = PC\) nên \(MB = MC.\)
Xét \(\Delta ABC\) có \(D,\,\,M\) lần lượt là trung điểm của \(AB,\,\,BC\) (do \(DB = DA,MB = MC)\) nên \(DM\) là đường trung bình của \(\Delta ABC.\)
Do đó \[DM = \frac{1}{2}AC\] (tính chất đường trung bình của tam giác).
Suy ra \(AC = 2DM = 2 \cdot 2,8 = 5,6{\rm{\;}}\left( {\rm{m}} \right).\) Hay \[y = 5,6{\rm{\;}}\left( {\rm{m}} \right).\]
Vậy độ dài của cây chống đứng bên và độ dài của của cánh kèo lần lượt là \(x = 1,35{\rm{\;}}\left( {\rm{m}} \right);\) \(y = 5,6{\rm{\;}}\left( {\rm{m}} \right).\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
a) Trong các mặt hàng trên, sản phẩm được giảm giá nhiều nhất là áo sơ mi giảm \(35\% ,\) sản phẩm được giảm giá ít nhất là quần Jean giảm \(10\% .\)
b) An nên dùng biểu đồ cột để biểu diễn.
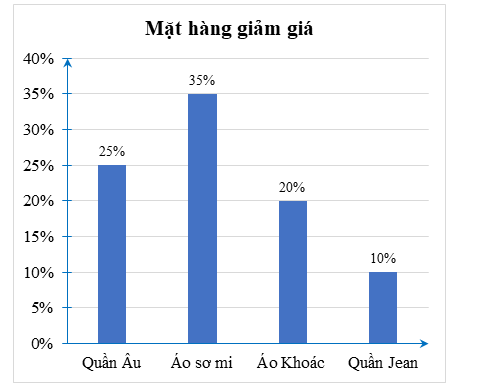
c) Áo sơ mi giảm \(35\% ,\) giá sau giảm là \(325\,\,000\) đồng. Do đó mỗi chiếc áo sơ mi nguyên giá sẽ là \(325\,\,000:65\% = 500\,\,000\) (đồng).
Giá một chiếc quần Âu sau giảm là \(\frac{{1\,\,850\,\,000 - 325\,\,000 \cdot 2}}{4} = 300\,\,000\) (đồng).
Quần âu giảm giá \(25\% ,\) do đó mỗi chiếc quần âu nguyên giá sẽ là
\(300\,\,000:75\% = 400\,\,000\) (đồng).
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
Xác suất thực nghiệm của biến cố “Quả bóng lấy ra là quả bóng màu xanh dương” là
\(\frac{{30 - 10 - 8}}{{30}} = \frac{{12}}{{30}} = \frac{2}{5}.\)
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập