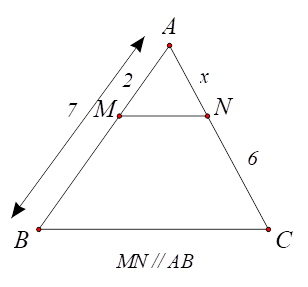Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
|
1) ⦁ Hình 1: Ta có \(MB = AB - AM = 7 - 2 = 5.\) Tam giác \(ABC\) có \(MN\,{\rm{//}}\,AB,\) theo định lí Thalès ta có: \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\) hay \(\frac{2}{5} = \frac{x}{6},\) suy ra \(x = \frac{{12}}{5}.\) Vậy \(x = \frac{{12}}{5}.\) |
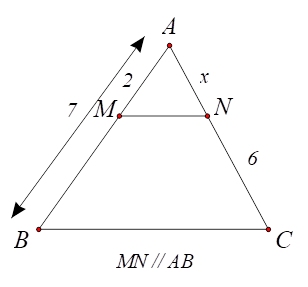
Hình 1
|
|
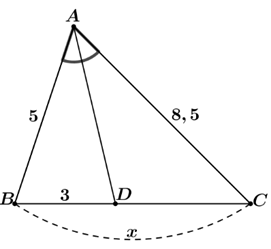
⦁ Hình 2: Xét tam giác \[ABC\] có \[AD\] là phân giác trong góc \[\widehat {BAC}\] (do \[\widehat {BAD} = \widehat {CAD}),\] nên \(\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}},\) hay \[\frac{{DB}}{{AB}} = \frac{{DC}}{{AC}}\] Do đó \[\frac{3}{5} = \frac{{DC}}{{8,5}},\] suy ra \[DC = \frac{{8,5 \cdot 3}}{5} = 5,1.\] Khi đó \(x = BC = DB + DC = 3 + 5,1 = 8,1.\) |
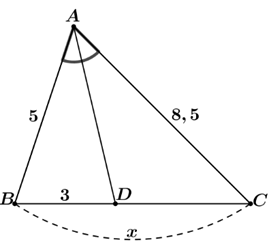 Hình 2 |
2)
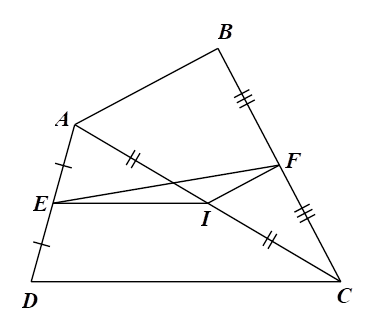
a) Xét \(\Delta ADC\) có \(E,\,\,I\) lần lượt là trung điểm của \(AD,\,\,AC\) nên \[EI\] là đường trung bình của \(\Delta ADC.\)
Do đó \(EI\,{\rm{//}}\,CD\) và \(EI = \frac{{C{\rm{D}}}}{2}.\)
Xét \(\Delta ABC\) có \(I,\,\,F\) lần lượt là trung điểm của \(AC,\,\,BC\) nên \[IF\] là đường trung bình của \(\Delta ABC.\)
Do đó \(IF\,{\rm{//}}\,AB\) và \(IF = \frac{{AB}}{2}.\)b) Trong \(\Delta EIF\) ta có: \(EF \le EI + IF\) (dấu "=" xảy ra khi \[E,\,\,I,\,\,F\] thẳng hàng)
Mà \(EI = \frac{{C{\rm{D}}}}{2};\,\,IF = \frac{{AB}}{2}\) (chứng minh ở câu a)
Do đó \[EF \le \frac{{AB + CD}}{2}.\]
Vậy \[EF \le \frac{{AB + CD}}{2}\] (dấu bằng xảy ra khi \(AB\,{\rm{//}}\,CD).\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
a) Ta lập bảng số liệu thống kê số giờ nắng của các tháng trong năm 2022 như sau:
|
Tháng |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Tổng số giờ nắng (h) |
\[34,4\] |
\[27,5\] |
\[49,4\] |
\[108,2\] |
\[88,8\] |
\[186,6\] |
\[190,7\] |
\[151,7\] |
\[133,2\] |
\[165,0\] |
\[126,2\] |
\[102,1\] |
Ta vẽ biểu đồ đoạn thẳng biểu diễn số giờ nắng của các tháng trong năm 2022 tại trạm quan trắc Nam Định như sau:
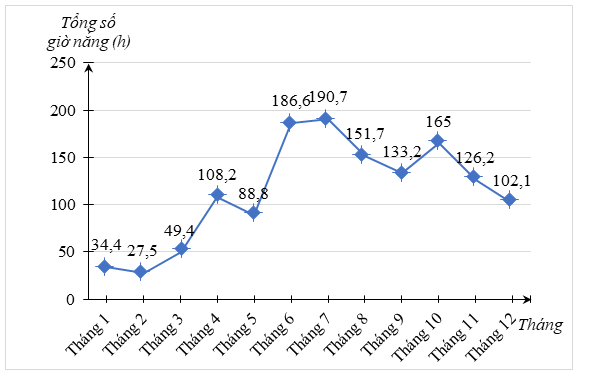
b) Số giờ nắng tại Nam Định trong tháng 7 là cao nhất \(\left( {190,7\,\,{\rm{h}}} \right)\) và tháng 2 là thấp nhất \(\left( {27,5\,\,{\rm{h}}} \right).\)
c) So với tháng 9, số giờ nắng tại Nam Định trong tháng 10 bằng \(\frac{{165}}{{133,2}} \cdot 100\% \approx 123,87\% .\)
Khi đó tháng 10 tăng khoảng \(123,87\% - 100\% = 23,87\% \) so với tháng 9.
Vậy thông tin của bài báo đó không chính xác.
Câu 2
A. Dữ liệu không là số, có thể sắp thứ tự.
B. Dữ liệu không là số, không thể sắp thứ tự.
C. Số liệu rời rạc.
D. Số liệu liên tục
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Dữ liệu thu được: Hài lòng, Rất hài lòng, Bình thường, Không hài lòng là dữ liệu không là số, có thể sắp thứ tự theo mức độ hài lòng về chất lượng dịch vụ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(24{\rm{\;c}}{{\rm{m}}^2}.\)
B. \(48{\rm{\;c}}{{\rm{m}}^2}.\)
C. \(12{\rm{\;c}}{{\rm{m}}^2}.\)
D. \(32{\rm{\;c}}{{\rm{m}}^2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\frac{5}{9}.\)
B. \(\frac{9}{5}.\)
C. \(\frac{9}{{14}}.\)
D. \[\frac{{14}}{9}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(x \approx 7,15{\rm{\;cm}}{\rm{.}}\)
B. \[x \approx 7,10{\rm{\;cm}}{\rm{.}}\]
C. \(x \approx 7,14{\rm{\;cm}}{\rm{.}}\)
D. \(x \approx 7,142{\rm{\;cm}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập