1) Tìm độ dài \[x,{\rm{ }}y\] trong mỗi trường hợp sau:
2) Cho tam giác \(ABC\) có \(AB = 4{\rm{\;cm}},\) \(AC = 5{\rm{\;cm}},\) \(BC = 6{\rm{\;cm}}.\) Các đường phân giác \(BD\) và \(CE\) cắt nhau tại \(I.\)
a) Tính \(AD,\,\,DC.\)
b) Tính các tỉ số \(\frac{{DI}}{{DB}},\,\,\frac{{BE}}{{BA}},\,\,\frac{{AD}}{{AC}}.\)
c) Tính tỉ số diện tích các tam giác \(DIE\) và \(ABC.\)
1) Tìm độ dài \[x,{\rm{ }}y\] trong mỗi trường hợp sau:
2) Cho tam giác \(ABC\) có \(AB = 4{\rm{\;cm}},\) \(AC = 5{\rm{\;cm}},\) \(BC = 6{\rm{\;cm}}.\) Các đường phân giác \(BD\) và \(CE\) cắt nhau tại \(I.\)
a) Tính \(AD,\,\,DC.\)
b) Tính các tỉ số \(\frac{{DI}}{{DB}},\,\,\frac{{BE}}{{BA}},\,\,\frac{{AD}}{{AC}}.\)
c) Tính tỉ số diện tích các tam giác \(DIE\) và \(ABC.\)
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
|
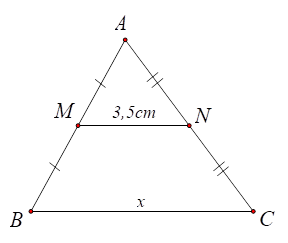
1) ⦁ Hình 1: Tam giác \[ABC\] có \[M,\,\,N\] lần lượt là trung điểm của \[AB\] và \[AC\] nên \[MN\] là đường trung bình của tam giác. Do đó \[MN = \frac{1}{2}BC.\] Suy ra \[x = BC = 2MN = 2 \cdot 3,5 = 7\left( {{\rm{cm}}} \right).\] Vậy \(x = 7{\rm{\;cm}}.\) |
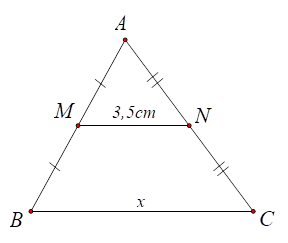 Hình 1 |
|
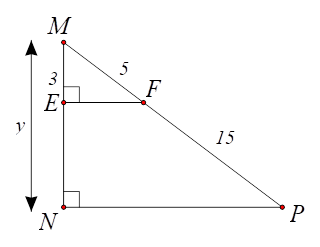
⦁ Hình 2: Ta có: \[EF \bot MN,\,\,NP \bot MN\] nên \[EF\,{\rm{//}}\,NP.\] \(MP = MF + FP = 5 + 15 = 20.\) Tam giác \[MNP\] có \[EF\,{\rm{//}}\,NP,\] theo định lí Thalès ta có: \[\frac{{ME}}{{MN}} = \frac{{MF}}{{MP}}\] hay \(\frac{3}{y} = \frac{5}{{20}},\) suy ra \(y = \frac{{3 \cdot 20}}{5} = 12.\) Vậy \(y = 12.\) |
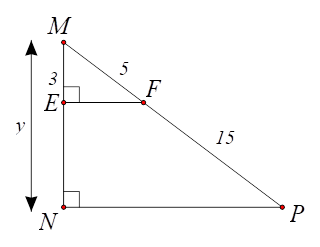 Hình 2 |
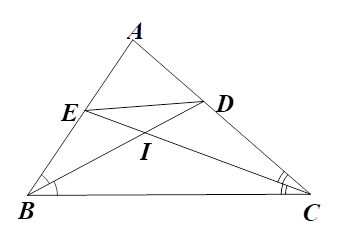
a) Xét \(\Delta ABC\) có \(BD\) là tia phân giác của \(\widehat {ABC}\) nên \[\frac{{BA}}{{BC}} = \frac{{DA}}{{DC}}\] (tính chất đường phân giác), do đó \[\frac{{DC}}{{BC}} = \frac{{DA}}{{BA}}.\]
Theo tính chất dãy tỉ số bằng nhau ta có \[\frac{{DC}}{{BC}} = \frac{{DA}}{{BA}} = \frac{{DC + DA}}{{BC + BA}} = \frac{{AC}}{{BC + BA}} = \frac{5}{{6 + 4}} = \frac{1}{2}.\]Do đó \(AD = \frac{1}{2}AB = \frac{1}{2} \cdot 4 = 2{\rm{\;cm}};\) \(DC = \frac{1}{2}BC = \frac{1}{2} \cdot 6 = 3{\rm{\;cm}}.\)
b) Xét \(\Delta BCD\) có \(CI\) là tia phân giác của \(\widehat {DCB}\) nên \[\frac{{DI}}{{BI}} = \frac{{DC}}{{BC}} = \frac{1}{2}\] (tính chất đường phân giác), suy ra \[\frac{{DI}}{{BI + DI}} = \frac{1}{{2 + 1}},\] hay \(\frac{{DI}}{{DB}} = \frac{1}{3}.\)
Chứng minh tương tự, ta cũng có:
⦁ \(\frac{{BE}}{{EA}} = \frac{{BC}}{{AC}} = \frac{6}{5},\) suy ra \(\frac{{BE}}{{BA}} = \frac{6}{{11}}.\)
⦁ \(\frac{{AD}}{{DC}} = \frac{{AB}}{{BC}} = \frac{6}{5},\) suy ra \(\frac{{AD}}{{AC}} = \frac{2}{5}.\)
c) Gọi \({h_1},\,\,{h_2},\,\,{h_3}\) lần lượt là độ dài đường cao kẻ từ \(E\) đến \(BD;\) độ dài đường cao kẻ từ \(D\) đến \(AB;\) độ dài đường cao kẻ từ \(B\) đến \(AC.\)
Ta có: \[{S_{DIE}} = \frac{1}{2} \cdot {h_1} \cdot DI;\] \({S_{BDE}} = \frac{1}{2}{h_1} \cdot BD = \frac{1}{2}{h_2} \cdot BE;\)
\({S_{ABD}} = \frac{1}{2}{h_2} \cdot AB = \frac{1}{2}{h_3} \cdot AD;\) \({S_{ABC}} = \frac{1}{2} \cdot {h_3} \cdot AC.\)
Do đó \[\frac{{{S_{DIE}}}}{{{S_{BDE}}}} = \frac{{\frac{1}{2} \cdot {h_1} \cdot DI}}{{\frac{1}{2}{h_1} \cdot BD}} = \frac{{DI}}{{BD}} = \frac{1}{3};\] \[\frac{{{S_{BDE}}}}{{{S_{ABD}}}} = \frac{{\frac{1}{2}{h_2} \cdot BE}}{{\frac{1}{2}{h_2} \cdot AB}} = \frac{{BE}}{{AB}} = \frac{6}{{11}};\]
\[\frac{{{S_{ABD}}}}{{{S_{ABC}}}} = \frac{{\frac{1}{2}{h_3} \cdot AD}}{{\frac{1}{2}{h_3} \cdot AC}} = \frac{{AD}}{{AC}} = \frac{2}{5}.\]
Khi đó \[{S_{DIE}} = \frac{1}{3}{S_{BDE}} = \frac{1}{3} \cdot \frac{6}{{11}}{S_{ABD}} = \frac{1}{3} \cdot \frac{6}{{11}} \cdot \frac{2}{5}{S_{ABC}} = \frac{4}{{55}}{S_{ABC}}.\]
Suy ra \(\frac{{{S_{DIE}}}}{{{S_{ABC}}}} = \frac{4}{{55}}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
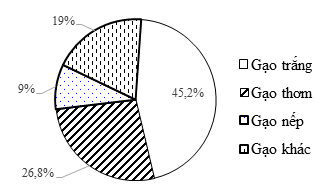
a) Ta lập được bảng thống kê như sau:
|
Loại gạo |
Tỉ lệ \(\left( \% \right)\) |
|
Gạo trắng |
\(45,2\) |
|
Gạo thơm |
\(26,8\) |
|
Gạo nếp |
\(9\) |
|
Gạo khác |
\(19\) |
b) Loại gạo xuất khẩu nhiều nhất là Gạo trắng, chiếm \(45,2\% .\)
Loại gạo xuất khẩu ít nhất là Gạo nếp, chiếm \(9\% .\)
c) Số lượng gạo thơm nước ta xuất khẩu trong năm \(2022\) là:
\(6,15 \cdot 26,8\% = 1,6482\) (triệu tấn).
d) Ta tính được lượng gạo trắng, gạo nếp, gạo khác lần lượt là \(2,7798\) triệu tấn; \(0,5535\) triệu tấn; \(1,1685\) triệu tấn.
Biểu đồ cột biểu diễn lượng gạo nước ta xuất khẩu được trong năm \(2022\) như sau:
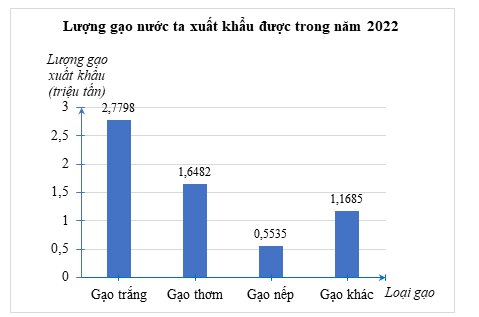
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
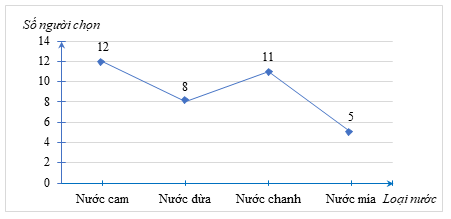
Số học sinh của lớp đó là: \(12 + 8 + 11 + 5 = 36\) (học sinh).
Loại nước được yêu thích nhất trong lớp là nước cam, với 12 học sinh lựa chọn.
Số học sinh chọn nước dừa nhiều hơn số học sinh chọn nước mía là \(8 - 5 = 3\) (học sinh).
Tổng số học sinh chọn nước dừa và nước mía là: \(8 + 5 = 13\) (học sinh), nhiều hơn số học sinh chọn nước cam. Do đó khẳng định D là sai.
Vậy ta chọn phương án D.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.