Chứng minh định lí là
A. Dùng hình vẽ để từ giả thiết suy ra kết luận.
B. Dùng đo đạc thực tế để suy ra kết luận từ giả thiết.
C. Dùng lập luận để từ giả thiết suy ra kết luận.
D. Cả A, B, C đều sai.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
Chứng minh định lí là dùng lập luận đề từ giả thiết suy ra kết luận.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. Nếu \(a\parallel b;{\rm{ }}b\parallel c\) thì \(a \bot c.\)
B. Nếu \(a \bot b;{\rm{ }}b \bot c\) thì \(a \bot c.\)
C. Nếu \(a \bot b;{\rm{ }}b\parallel c\) thì \(a\parallel c.\)
D. Nếu \(a\parallel b;{\rm{ }}b\parallel c\) thì \(a\parallel c.\)
Lời giải
Đáp án đúng là: D
Ta có định lí: “Nếu hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chung song song với nhau”.
Hay nếu \(a\parallel b;{\rm{ }}b\parallel c\) thì \(a\parallel c.\)
Lời giải
Khẳng định đúng là (I) và (III) vì ta có:
Nếu \(Ot\) là tia phân giác của \(\widehat {aOb}\) thì \(\widehat {aOt} = \widehat {tOb} = \frac{1}{2}\widehat {aOb}\).
Câu 3
A. “Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba”.
B. “Chúng song song với nhau”.
C. “Hai đường thẳng phân biệt cùng vuông góc”.
D. “Hai đường thẳng phân biệt”.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
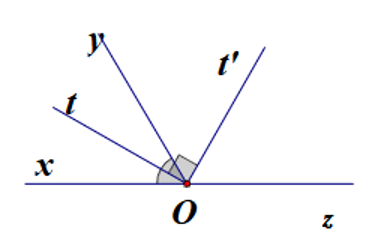
a) Giả thiết của bài toán là \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù; \(Ot\) là tia phân giác của \(\widehat {xOy}\).
Đúng
Sai
b) Kết luận của bài toán là “\(Ot'\) là tia phân giác của \(\widehat {zOy}\)”.
Đúng
Sai
c) \(\widehat {xOt} = \widehat {tOy}.\)
Đúng
Sai
d) \(\widehat {zOt'} = \widehat {t'Oy}.\)
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
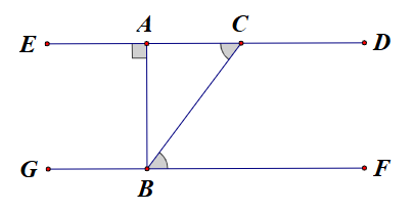
a) \(\widehat {ACB},\,\,\widehat {CBF}\) là hai góc ở vị trí so le trong.
Đúng
Sai
b) \(ED\) không song song với \(GF.\)
Đúng
Sai
c) \(\widehat {ABF} = 90^\circ \)
Đúng
Sai
d) \(AB \bot \,GF\).
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
a) \(\widehat A + \widehat B + \widehat C = 180^\circ \).
Đúng
Sai
b) \(\widehat A = 90^\circ - \widehat C\).
Đúng
Sai
c) \(\widehat A - \widehat B = 2\widehat C\).
Đúng
Sai
d) \(\widehat A = \widehat B\).
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập