Người ta bắn một viên bi với vận tốc ban đầu 4 m/s hướng lên theo phương xiên 45o so với phương nằm ngang. Coi sức cản của không khí là không đáng kể.
1. Tính vận tốc của viên bi theo phương nằm ngang và phương thẳng đứng tại các thời điểm: bắt đầu bắn, sau 0,1 s và sau 0,2 s.
2. a) Viên bi đạt tầm cao H vào lúc nào?
b) Tính tầm cao H.
c) Gia tốc của viên bi ở tầm cao H có giá trị bằng bao nhiêu?
3. a) Vận tốc của viên bi có độ lớn cực tiểu ở vị trí nào?
b) Viên bi có vận tốc cực tiểu vào thời điểm nào?
4. a) Khi nào viên bi chạm sàn?
b) Xác định vận tốc của viên bi khi chạm sàn?
c) Xác định tầm xa L của viên bi.
Người ta bắn một viên bi với vận tốc ban đầu 4 m/s hướng lên theo phương xiên 45o so với phương nằm ngang. Coi sức cản của không khí là không đáng kể.
1. Tính vận tốc của viên bi theo phương nằm ngang và phương thẳng đứng tại các thời điểm: bắt đầu bắn, sau 0,1 s và sau 0,2 s.
2. a) Viên bi đạt tầm cao H vào lúc nào?
b) Tính tầm cao H.
c) Gia tốc của viên bi ở tầm cao H có giá trị bằng bao nhiêu?
3. a) Vận tốc của viên bi có độ lớn cực tiểu ở vị trí nào?
b) Viên bi có vận tốc cực tiểu vào thời điểm nào?
4. a) Khi nào viên bi chạm sàn?
b) Xác định vận tốc của viên bi khi chạm sàn?
c) Xác định tầm xa L của viên bi.
Câu hỏi trong đề: 10000 câu trắc nghiệm tổng hợp Vật lí 2025 có đáp án !!
Quảng cáo
Trả lời:
Lời giải:
Chọn hệ trục tọa độ phân tích chuyển động ném xiên như hình dưới
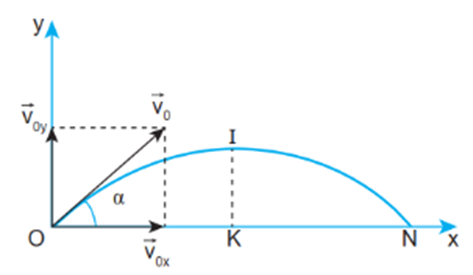
1.
- Thời điểm bắt đầu bắn:
- Vận tốc theo phương ngang: \({v_{0x}} = {v_0}\cos {45^^\circ } = 4 \cdot \frac{{\sqrt 2 }}{2} = 2\sqrt 2 {\rm{ m/s}}\)
- Vận tốc theo phương thẳng đứng: \({v_{0y}} = {v_0}\sin {45^^\circ } = 4 \cdot \frac{{\sqrt 2 }}{2} = 2\sqrt 2 {\rm{ m/s}}\)
- Sau 0,1 s:
- Vận tốc theo phương ngang: \({v_x} = {v_{0x}} = 2\sqrt 2 {\rm{ m/s}}\) (chuyển động thành phần theo phương ngang là chuyển động thẳng đều)
- Vận tốc theo phương thẳng đứng: \({v_y} = {v_{0y}} - gt = 2\sqrt 2 - 9,8 \cdot 0,1 = 1,85{\rm{ m/s}}\)
- Sau 0,2 s:
- Vận tốc theo phương ngang: \({v_x} = {v_{0x}} = 2\sqrt 2 {\rm{ m/s}}\) (chuyển động thành phần theo phương ngang là chuyển động thẳng đều)
- Vận tốc theo phương thẳng đứng: \({v_y} = {v_{0y}} - gt = 2\sqrt 2 - 9,8 \cdot 0,2 = 0,87{\rm{ m/s}}\)
2.
a) Khi đạt tới tầm cao H thì: \({v_y} = {v_{0y}} - gt = 0 \Rightarrow t = \frac{{{v_{0y}}}}{g} = \frac{{2\sqrt 2 }}{{9,8}} = 0,289{\rm{ s}}\)
b) Tầm cao H là: \(H = \frac{{v_{0y}^2}}{{2g}} = \frac{{{{(2\sqrt 2 )}^2}}}{{2 \cdot 9,8}} = 0,408{\rm{ m}}\)
c) Gia tốc của viên bi ở tầm cao \(H\): \(a = g = 9,8{\rm{ m/}}{{\rm{s}}^2}\) vì khi vật đạt độ cao max vận tốc của vật bằng \(0\) và vật rơi xuống do chịu tác dụng của trọng lực.
3.
a) Vận tốc của viên bi có độ lớn cực tiểu ở vị trí tầm cao \(H = 0,408{\rm{ m}}\)
b) Viên bi có vận tốc cực tiểu vào thời điểm vật bắt đầu chạm sàn vì khi đó vật bay ngược chiều dương đã chọn và vận tốc có giá trị âm:
\(t' = 2t = 2 \cdot 0,289 = 0,578{\rm{ s}}\)
4.
a) Khi viên bi chạm sàn thì thời gian chuyển động (gấp 2 lần thời gian từ lúc bắt đầu ném cho đến khi đạt tầm cao H) là:
\(t' = 2t = \frac{{2 \cdot {v_{0y}}}}{g} = 2 \cdot 0,289 = 0,578{\rm{ s}}\)
b) Khi chạm sàn: \(v = \sqrt {v_x^2 + v_y^2} \)
- Thành phần chuyển động theo phương ngang: \({v_x} = {v_{0x}} = 2\sqrt 2 {\rm{ m/s}}\)
- Thành phần chuyển động theo phương thẳng đứng: \({v_y} = \sqrt {2gH} \)
Suy ra: \(v = \sqrt {v_{0x}^2 + 2gH} = \sqrt {{{(2\sqrt 2 )}^2} + 2 \cdot 9,8 \cdot 0,408} \approx 4{\rm{ m/s}}\)
c) Tầm xa: \(L = {d_{x{\rm{ max}}}} = {v_{0x}} \cdot t' = 2\sqrt 2 \cdot 0,578 = 1,635{\rm{ m}}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
\[c\'o \;M = \frac{m}{n} = \frac{{m.22,4}}{V} = \frac{{m.22,4}}{{m/D}} = D*22,4\]
\( = > D = \frac{M}{{22,4}}\)
\({M_1} = {29.10^{ - 3}}\)
\({T_1} = 273K\)
\({M_2} = ?\)
\({T_2} = 300K\)
\(c\'o :\;\frac{{{D_1}}}{{{D_2}}} = \frac{{{T_2}}}{{{T_1}\;}} = > \;\frac{{{M_1}}}{{{M_2}}} = \frac{{{T_2}}}{{{T_1}}}\; = > \;{M_2}\~0,026\)
\[{D_2} = \frac{{{M_2}}}{{22,4}}\; = > \;{D_2} = \;1,178\left( {kg/{m^3}} \right)\]
Lời giải
Lời giải:
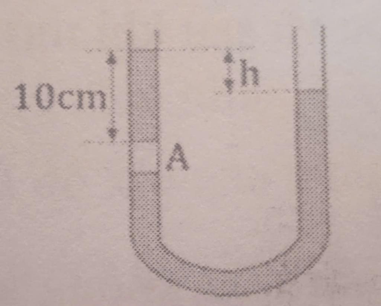
Để cột khí đứng yên thì áp suất do thủy ngân bên trên cân bằng với áp suất do bên dưới gây ra:
\({p_C} = {p_B} = {h_C} + {p_0}\)
Áp suất chất lỏng đứng yên tại cùng mức ngang thì bằng nhau:
\({p_B} = {p_D} = {h_D} + {p_0}\)
Do đó ta suy ra: \({p_B} = {p_C} = {p_B} = {h_C} + {p_0} = {h_D} + {p_0}\)
\( \Rightarrow {h_C} = {h_D} = 10{\rm{ (cm)}}\)
Độ cao chênh lệch của mặt thủy ngân là:
\(\Delta h = {h_B} - {h_D} = (10 + 2) - 10 = 2{\rm{ (cm)}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.