Một lượng không khí có thể tích \({V_1} = 240{\rm{ c}}{{\rm{m}}^3}\) bị giam trong một xilanh có pít-tông đóng kín, diện tích của pít-tông là \(S = 24{\rm{ c}}{{\rm{m}}^2}\). Áp suất khí trong xilanh bằng áp suất ngoài là \({p_1} = 100{\rm{ kPa}}\). Cần một lực bằng bao nhiêu để dịch chuyển pít-tông sang trái \(d = 2{\rm{ cm}}\)? Bỏ qua mọi ma sát, coi quá trình trên là đẳng nhiệt.
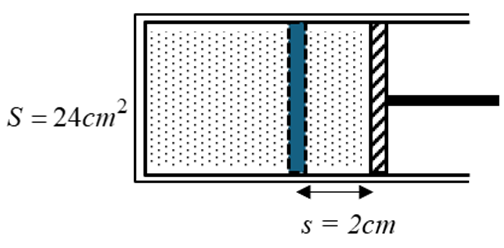
Một lượng không khí có thể tích \({V_1} = 240{\rm{ c}}{{\rm{m}}^3}\) bị giam trong một xilanh có pít-tông đóng kín, diện tích của pít-tông là \(S = 24{\rm{ c}}{{\rm{m}}^2}\). Áp suất khí trong xilanh bằng áp suất ngoài là \({p_1} = 100{\rm{ kPa}}\). Cần một lực bằng bao nhiêu để dịch chuyển pít-tông sang trái \(d = 2{\rm{ cm}}\)? Bỏ qua mọi ma sát, coi quá trình trên là đẳng nhiệt.
A. \(60{\rm{N}}\)
B. \(40{\rm{N}}\)
C. \(20{\rm{N}}\)
D. \(10{\rm{N}}\)
Câu hỏi trong đề: 10000 câu trắc nghiệm tổng hợp Vật lí 2025 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải:
Trạng thái 1: \(\left\{ {\begin{array}{*{20}{l}}{{V_1} = 240{\rm{ c}}{{\rm{m}}^3}}\\{{p_1} = 100{\rm{ kPa}} = {{10}^5}{\rm{ Pa}}}\end{array}} \right.\)
Khi pít – tông dịch chuyển sang trái \(2{\rm{ cm}}\)
\( \Rightarrow \) Thể tích của khí giảm: \(\Delta V = s.S = 2.24 = 48{\rm{ c}}{{\rm{m}}^3}\)
Trạng thái 2: \(\left\{ {\begin{array}{*{20}{l}}{{V_2} = {V_1} - \Delta V = 240 - 48 = 192{\rm{ c}}{{\rm{m}}^3}}\\{{p_2} = ?}\end{array}} \right.\)
Quá trình biến đổi trạng thái là quá trình đẳng nhiệt, ta có:
\({p_1}{V_1} = {p_2}.{V_2} \Rightarrow {p_2} = \frac{{{p_1}{V_1}}}{{{V_2}}} = \frac{{{{10}^5}.240}}{{192}} = {1,25.10^5}{\rm{ Pa}}\)
Lực cần đẩy pittong là:
\(F = \Delta p.S = ({p_2} - {p_1}).S = ({1,25.10^5} - {10^5}){.24.10^{ - 4}} = 60{\rm{ (N)}}\)
Đáp án cần chọn là: A
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- 500 Bài tập tổng ôn Vật lí (Form 2025) ( 38.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
\[c\'o \;M = \frac{m}{n} = \frac{{m.22,4}}{V} = \frac{{m.22,4}}{{m/D}} = D*22,4\]
\( = > D = \frac{M}{{22,4}}\)
\({M_1} = {29.10^{ - 3}}\)
\({T_1} = 273K\)
\({M_2} = ?\)
\({T_2} = 300K\)
\(c\'o :\;\frac{{{D_1}}}{{{D_2}}} = \frac{{{T_2}}}{{{T_1}\;}} = > \;\frac{{{M_1}}}{{{M_2}}} = \frac{{{T_2}}}{{{T_1}}}\; = > \;{M_2}\~0,026\)
\[{D_2} = \frac{{{M_2}}}{{22,4}}\; = > \;{D_2} = \;1,178\left( {kg/{m^3}} \right)\]
Lời giải
Lời giải:
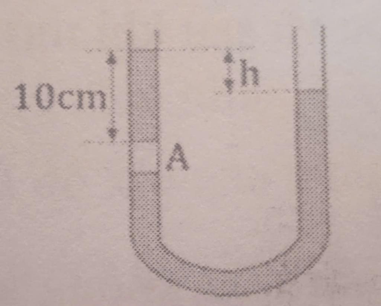
Để cột khí đứng yên thì áp suất do thủy ngân bên trên cân bằng với áp suất do bên dưới gây ra:
\({p_C} = {p_B} = {h_C} + {p_0}\)
Áp suất chất lỏng đứng yên tại cùng mức ngang thì bằng nhau:
\({p_B} = {p_D} = {h_D} + {p_0}\)
Do đó ta suy ra: \({p_B} = {p_C} = {p_B} = {h_C} + {p_0} = {h_D} + {p_0}\)
\( \Rightarrow {h_C} = {h_D} = 10{\rm{ (cm)}}\)
Độ cao chênh lệch của mặt thủy ngân là:
\(\Delta h = {h_B} - {h_D} = (10 + 2) - 10 = 2{\rm{ (cm)}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. nhận công và tăng nhiệt độ.
B. thực hiện công và tăng nhiệt độ.
C. thực hiện công và giảm nhiệt độ.
D. nhận công và giảm nhiệt độ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập