Một ca nô chạy qua sông xuất phát từ \(A\), mũi hướng tới điểm \(B\) ở bờ bên kia. AB vuông góc với bờ sông. Nhưng do nước chảy nên khi đến bờ bên kia, ca nô lại ở cách \(B\) đoạn \(240{\rm{ m}}\). Thời gian qua sông là 120 giây. Nếu người lái giữ cho mũi ca nô chếch 30oC so với bờ sông và mở máy chạy như trước thì ca nô chạy tới đúng điểm \(B\). Tính:
a) Vận tốc nước chảy so với bờ và vận tốc ca nô so với nước.
b) Bề rộng dòng sông.
c) Thời gian qua sông của ca nô lần sau.
Một ca nô chạy qua sông xuất phát từ \(A\), mũi hướng tới điểm \(B\) ở bờ bên kia. AB vuông góc với bờ sông. Nhưng do nước chảy nên khi đến bờ bên kia, ca nô lại ở cách \(B\) đoạn \(240{\rm{ m}}\). Thời gian qua sông là 120 giây. Nếu người lái giữ cho mũi ca nô chếch 30oC so với bờ sông và mở máy chạy như trước thì ca nô chạy tới đúng điểm \(B\). Tính:
a) Vận tốc nước chảy so với bờ và vận tốc ca nô so với nước.
b) Bề rộng dòng sông.
c) Thời gian qua sông của ca nô lần sau.
Câu hỏi trong đề: 10000 câu trắc nghiệm tổng hợp Vật lí 2025 có đáp án !!
Quảng cáo
Trả lời:
Lời giải:
Gọi vận tốc ca nô so với nước và vận tốc của nước so với bờ lần lượt là \({v_1}\), \({v_2}\).
Ta có hình vẽ:
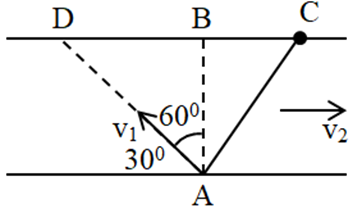
a) + Trong lần chuyển động đầu tiên:
Thời gian ca nô chuyển động từ \(A\) đến \(C\) khi nước chảy bằng thời gian nước chảy từ 1\(B\) đến 2\(C\) và bằng thời gian ca nô đi từ 3\(A\) đến 4\(B\) khi nước lặng:5
\({t_1} = \frac{{BC}}{{{v_2}}} \Rightarrow {v_2} = \frac{{BC}}{{{t_1}}} = \frac{{240}}{{120}} = 2{\rm{ (m/s)}}\)
\({t_1} = \frac{{AB}}{{{v_1}}}\quad (1)\)
+ Trong lần chuyển động thứ hai:
Thời gian ca nô chuyển động từ \(A\) đến \(B\) khi nước chảy bằng thời gian nước chảy từ \(D\) đến \(B\) và bằng thời gian ca nô chuyển động từ \(A\) đến \(D\) khi nước lặng:
\({t_2} = \frac{{DB}}{{{v_2}}} = \frac{{AD}}{{{v_1}}} \Rightarrow \frac{{DB}}{{AD}} = \frac{{{v_2}}}{{{v_1}}}\)
Xét tam giác vuông ABD, ta có:
\(\sin {60^^\circ } = \frac{{BD}}{{AD}} = \frac{{{v_2}}}{{{v_1}}} \Rightarrow {v_1} = \frac{{{v_2}}}{{\sin {{60}^^\circ }}} = \frac{2}{{\sin {{60}^^\circ }}} \approx 2,3{\rm{ (m/s)}}\)
b) Thay vào (1), ta có: \({t_1} = \frac{{AB}}{{{v_1}}} \Rightarrow 120 = \frac{{AB}}{{2,3}} \Rightarrow AB = 276{\rm{ (m)}}\)
c) Lại có: \(\cos {60^^\circ } = \frac{{AB}}{{AD}} = \frac{{276}}{{AD}} \Rightarrow AD = \frac{{276}}{{\cos {{60}^^\circ }}} = 552{\rm{ (m)}}\)
Thời gian ca nô qua sông lần sau là: \({t_2} = \frac{{AD}}{{{v_1}}} = \frac{{552}}{{2,3}} = 240{\rm{ (s)}} = 4{\rm{ (ph\'u t)}}\)
Đáp án cần chọn là: D
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
\[c\'o \;M = \frac{m}{n} = \frac{{m.22,4}}{V} = \frac{{m.22,4}}{{m/D}} = D*22,4\]
\( = > D = \frac{M}{{22,4}}\)
\({M_1} = {29.10^{ - 3}}\)
\({T_1} = 273K\)
\({M_2} = ?\)
\({T_2} = 300K\)
\(c\'o :\;\frac{{{D_1}}}{{{D_2}}} = \frac{{{T_2}}}{{{T_1}\;}} = > \;\frac{{{M_1}}}{{{M_2}}} = \frac{{{T_2}}}{{{T_1}}}\; = > \;{M_2}\~0,026\)
\[{D_2} = \frac{{{M_2}}}{{22,4}}\; = > \;{D_2} = \;1,178\left( {kg/{m^3}} \right)\]
Lời giải
Lời giải:
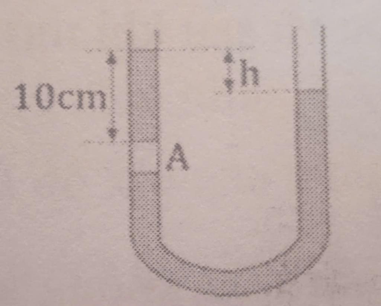
Để cột khí đứng yên thì áp suất do thủy ngân bên trên cân bằng với áp suất do bên dưới gây ra:
\({p_C} = {p_B} = {h_C} + {p_0}\)
Áp suất chất lỏng đứng yên tại cùng mức ngang thì bằng nhau:
\({p_B} = {p_D} = {h_D} + {p_0}\)
Do đó ta suy ra: \({p_B} = {p_C} = {p_B} = {h_C} + {p_0} = {h_D} + {p_0}\)
\( \Rightarrow {h_C} = {h_D} = 10{\rm{ (cm)}}\)
Độ cao chênh lệch của mặt thủy ngân là:
\(\Delta h = {h_B} - {h_D} = (10 + 2) - 10 = 2{\rm{ (cm)}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.