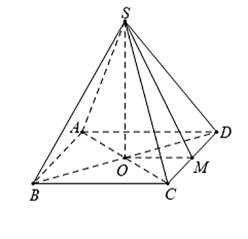
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật với \(AB = 4a\,,\,\,BC = 2a.\) Đỉnh \(S\) cách đều các đỉnh \[A,\,\,B,\,\,C,\,\,D.\] Biết góc giữa mặt phẳng \(\left( {SCD} \right)\) và \(\left( {ABCD} \right)\) bằng \(60^\circ .\) Thể tích khối chóp đã cho bằng:
A. \(\frac{{8\sqrt 3 {a^3}}}{3}.\)
B. \(\frac{{4{a^3}}}{3}.\)
C. \(8\sqrt 3 {a^3}.\)
D. \(4{a^3}.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi \(O\) là tâm của hình chữ nhật \(ABCD\).
Suy ra \(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot CD\).
Gọi \(M\) là trung điểm của \(CD \Rightarrow OM \bot CD\)
Do đó \(CD \bot \left( {SMO} \right)\) mà \(\left\{ {\begin{array}{*{20}{l}}{\left( {SMO} \right) \cap \left( {SCD} \right) = SM}\\{\left( {SMO} \right) \cap \left( {ABCD} \right) = OM}\end{array}} \right.\)
Suy ra \(\left( {\left( {SCD} \right),\,\,\left( {ABCD} \right)} \right) = \left( {SM,OM} \right) = \widehat {SMO} = 60^\circ .\)Ta có \(OM = \frac{1}{2}BC = \frac{1}{2} \cdot 2a = a \Rightarrow SO = OM \cdot \tan \widehat {SMO}\)
\( \Rightarrow SO = \sqrt 3 a \Rightarrow {V_{S \cdot ABCD}} = \frac{1}{3} \cdot SO \cdot {S_{ABCD}} = \frac{1}{3} \cdot \sqrt 3 a \cdot 8{a^2} = \frac{{8\sqrt 3 {a^3}}}{3}.\) Chọn A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. Hai luồng: trí thức và tầng lớp quý tộc địa phương.
B. Hai luồng: thường dân và trí thức.
C. Hai luồng: tầng lớp quý tộc địa phương, trí thức và thường dân.
D. Ba luồng: trí thức, thường dân và tầng lớp quý tộc địa phương.
Lời giải
Dựa vào câu văn đầu đoạn: Du nhập vào Thăng Long khá phức tạp nhưng có thể chia thành hai nhóm chính: Thứ nhất là trí thức và tầng lớp quý tộc địa phương, thứ hai là thường dân. Chọn C.
Câu 2
A. Tự sự.
B. Biểu cảm.
C. Miêu tả.
D. Thuyết minh.
Lời giải
Phương thức biểu đạt chính của đoạn trích là tự sự. Chọn A.
Câu 3
A. innovation.
B. advance.
C. progress.
D. reform.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Đau xót, bi ai.
B. Sâu lắng, buồn man mác.
C. Bi thương, uất hận.
D. Tiếc nuối, xót xa.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Cạnh tranh cùng loài.
B. Hỗ trợ cùng loài.
C. Đối kháng giữa các loài.
D. Hỗ trợ giữa các loài.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Chứng minh.
B. Bác bỏ.
C. Giải thích.
D. So sánh.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. the Taj Mahal receives about five million tourists every year.
B. the Taj Mahal is newly built, so it is called new wonder.
C. the Taj Mahal is made of white marble.
D. most visitors to the Taj Mahal are Indians.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập