Từ một đỉnh tháp cao 40 m so với mặt đất người ta ném một quả cầu theo phương ngang với tốc độ v0 = 10 m/s. Bỏ qua sức cản không khí, lấy g = 10 m/s2
a) Viết phương trình toạ độ của quả cầu và xác định toạ độ của quả cầu sau khi ném 2s.
b) Viết phương trình quỹ đạo của quả cầu và cho biết dạng quỹ đạo của quả cầu.
c) Quả cầu chạm đất ở vị trí nào? Tốc độ quả cầu khi chạm đất là bao nhiêu?
Câu hỏi trong đề: 10000 câu trắc nghiệm tổng hợp Vật lí 2025 có đáp án !!
Quảng cáo
Trả lời:
Lời giải:
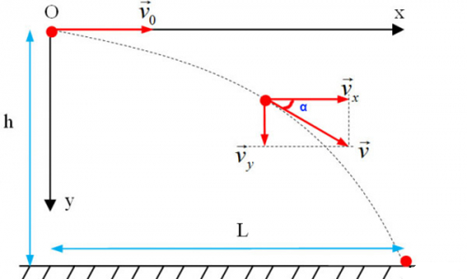
a, Theo phương Ox, vật chuyển động thẳng đều với vận tốc \({v_0} = 10m/s\).
Theo phương Oy, vật chuyển động như vật rơi tự do gia tốc \(g\).
PT toạ độ của vật: \(\left\{ {\begin{array}{*{20}{l}}{Ox:x = 10t,m{\rm{ (1)}}}\\{Oy:y = \frac{1}{2}g{t^2} = 5{t^2},m{\rm{ (2)}}}\end{array}} \right.\)
Với \(t' = 2s\) ta có:
\(\left\{ {\begin{array}{*{20}{l}}{Ox:x = 10.2 = 20m}\\{Oy:y = {{5.2}^2} = 20m}\end{array}} \right.\)
b, Từ (1) \( = > t = \frac{x}{{10}}\) thay vào (2) ta có:
\(y = 5 \cdot \frac{{{x^2}}}{{{{10}^2}}} = 0,05{x^2},m\)
Vậy PT quỹ đạo là \(y = 0,05{x^2}\), có dạng parabol.
c, Quả cầu chạm đất khi \(y = 40m\) (do tháp cao 40m)
\( = > 5.{t^2} = 40 < = > {t^2} = 8 < = > t = 2\sqrt 2 \), do \(t > 0\).
Khi đó: \({v_y} = gt = 10.2\sqrt 2 = 20\sqrt 2 m/s\)
\({v_x} = {v_0} = 10m/s\)
\( = > v = \sqrt {v_x^2 + v_y^2} = \sqrt {{{10}^2} + {{(20\sqrt 2 )}^2}} = 30m/s\)
Vậy vật chạm đất sau \(t = 2\sqrt 2 \) s với vận tốc chạm đất là \(30m/s\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
\[c\'o \;M = \frac{m}{n} = \frac{{m.22,4}}{V} = \frac{{m.22,4}}{{m/D}} = D*22,4\]
\( = > D = \frac{M}{{22,4}}\)
\({M_1} = {29.10^{ - 3}}\)
\({T_1} = 273K\)
\({M_2} = ?\)
\({T_2} = 300K\)
\(c\'o :\;\frac{{{D_1}}}{{{D_2}}} = \frac{{{T_2}}}{{{T_1}\;}} = > \;\frac{{{M_1}}}{{{M_2}}} = \frac{{{T_2}}}{{{T_1}}}\; = > \;{M_2}\~0,026\)
\[{D_2} = \frac{{{M_2}}}{{22,4}}\; = > \;{D_2} = \;1,178\left( {kg/{m^3}} \right)\]
Lời giải
Lời giải:
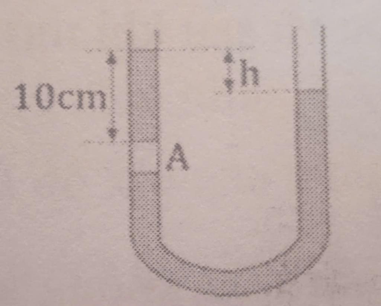
Để cột khí đứng yên thì áp suất do thủy ngân bên trên cân bằng với áp suất do bên dưới gây ra:
\({p_C} = {p_B} = {h_C} + {p_0}\)
Áp suất chất lỏng đứng yên tại cùng mức ngang thì bằng nhau:
\({p_B} = {p_D} = {h_D} + {p_0}\)
Do đó ta suy ra: \({p_B} = {p_C} = {p_B} = {h_C} + {p_0} = {h_D} + {p_0}\)
\( \Rightarrow {h_C} = {h_D} = 10{\rm{ (cm)}}\)
Độ cao chênh lệch của mặt thủy ngân là:
\(\Delta h = {h_B} - {h_D} = (10 + 2) - 10 = 2{\rm{ (cm)}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.