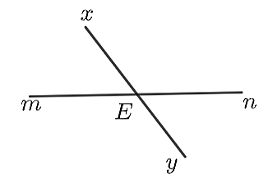
Cho hai đường thẳng \[a\] và \[b\] giao nhau tại \[O.\] Biết \[\widehat {{O_1}} = 30^\circ \], số đo của \[\widehat {{O_2}}\] là
Cho hai đường thẳng \[a\] và \[b\] giao nhau tại \[O.\] Biết \[\widehat {{O_1}} = 30^\circ \], số đo của \[\widehat {{O_2}}\] là
A. \[35^\circ .\]
B. \[150^\circ .\]
Quảng cáo
Trả lời:
Đáp án đúng là: D
Ta có \[\widehat {{O_2}} = \widehat {{O_1}} = 30^\circ \] (hai góc đối đỉnh).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
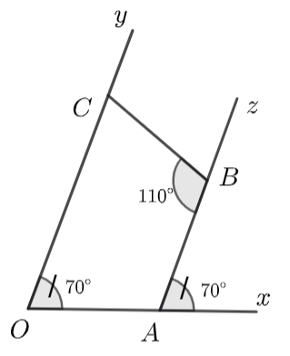
a) \(\widehat {ABC}\) và \(\widehat {CBz}\) là hai góc kề bù.
b) \(\widehat {CBz} = 70^\circ \).
c) \(Oy\) song song với \(Az\).
Lời giải
a) Đúng.
Nhận thấy \(\widehat {ABC}\) và \(\widehat {CBz}\) là hai góc kề bù nên ta có \(\widehat {CBz} + \widehat {ABC} = 180^\circ \). Do đó, ý a) đúng.
b) Đúng.
Suy ra \(\widehat {CBz} = 180^\circ - \widehat {CBA} = 180^\circ - 110^\circ = 70^\circ \). Do đó, ý b) đúng.
Ta có \(\widehat {xAz} = \widehat {xOy} = 70^\circ \).
c) Đúng.
Mà hai góc ở vị trí đồng vị nên \(Oy\parallel Az\). Do đó, ý c) đúng.
d) Sai.
Vì \(Oy\parallel Az\) nên \(\widehat {OCB} = \widehat {CBz} = 70^\circ \) (so le trong). Do đó, ý d) sai.
Câu 2
Lời giải
Đáp án đúng là: C
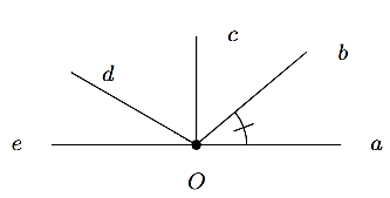
Góc kề bù với \(\widehat {aOb}\) là \(\widehat {eOb}.\)
Câu 3
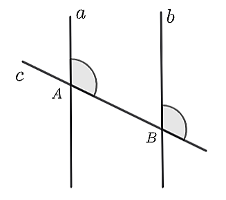
A. \(a\parallel b\) vì hai góc đồng vị bằng nhau.
B. \(a\parallel b\) vì hai góc so le trong bằng nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
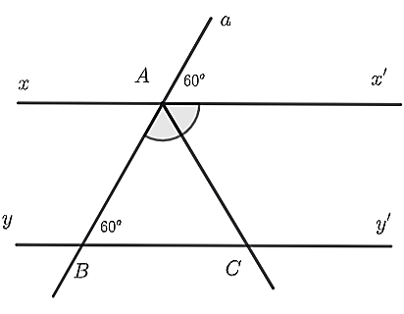
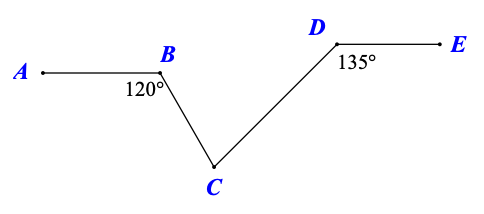
a) \(\widehat {aAx'}\) và \(\widehat {ABC}\) là hai góc so le trong.
b) \(x'x\parallel yy'.\)
c) \(\widehat {BAx'} = 120^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
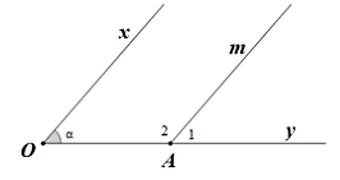
a) \(\widehat {{A_1}}\) và \(\widehat {{A_2}}\) là hai góc kề bù.
b) \(\widehat {{A_1}} = 60^\circ \).
c) \(\widehat {{A_1}}\) và \(\widehat {xOy}\) ở vị trí so le trong.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.