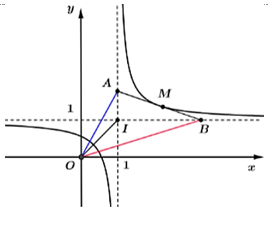
Cho hàm số \(y = \frac{{2x - 1}}{{2x - 2}}\) có đồ thị \(\left( C \right)\). Gọi \(M\left( {{x_0};{y_0}} \right)\) (với \({x_0} > 1\)) là điểm thuộc \(\left( C \right)\), biết tiếp tuyến của \(\left( C \right)\) tại \(M\) cắt tiệm cận đứng và tiệm cận ngang lần lượt tại \(A\) và \(B\) sao cho \({S_{OIB}} = 8{S_{OIA}}\) (trong đó \(O\) là gốc tọa độ, \(I\) là giao điểm hai tiệm cận). Tính giá trị của \(S = {x_0} + 4{y_0}\) (nhập đáp án vào ô trống).

Đáp án  __

Xét hàm số \(g\left( t \right) = {4^t} + {3^t} - 5t - 2\) trên \(\mathbb{R}\).

\(g'\left( t \right) = {4^t} \cdot \ln 4 + {3^t} \cdot \ln 3 - 5\,;\,\,g''\left( t \right) = {4^t} \cdot {\ln ^2}4 + {3^t} \cdot {\ln ^2}3 > 0\,\,\forall t \in \mathbb{R}\)

\( \Rightarrow \) Phương trình \(g\left( t \right) = 0\) có tối đa 2 nghiệm.

Mà \(g\left( 0 \right) = g\left( 1 \right) = 0\) nên phương trình \({4^{f\left( x \right) - m}} + {3^{f\left( x \right) - m}} - 5f\left( x \right) + 5m - 2 = 0\)

\( \Leftrightarrow g\left( {f\left( x \right) - m} \right) = 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{f\left( x \right) - m = 0}\\{f\left( x \right) - m = 1}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{f\left( x \right) = m}\\{f\left( x \right) = m + 1}\end{array}} \right.} \right.\).

Yêu cầu bài toán \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{ - 1 \le m \le 1}\\{ - 1 \le m + 1 \le 1}\end{array} \Leftrightarrow - 2 \le m \le 1} \right.\).

Do \(m\) nguyên nên \(m \in \left\{ { - 2\,;\,\, - 1\,;\,\,0\,;\,\,1} \right\}.\)

Vậy có 4 giá trị nguyên của tham số \(m\) thoả mãn yêu cầu bài toán. Chọn D.

TH1: Chọn 3 học sinh nữ có \(C_{15}^3 = 455\) (cách).

TH2: Chọn 2 học sinh nữ, 1 học sinh nam có \(C_{15}^2 \cdot C_{25}^1 = 2\,\,625\) (cách).

Số cách chọn 3 học sinh trong đó có nhiều nhất 1 học sinh nam là:

\[2\,\,625 + 455 = 3\,\,080\] (cách). Chọn D.