Bảng tần số ghép nhóm sau cho biết cân nặng của một số con voi khi vừa sinh ra (đơn vị tính là kg ):
Cân nặng (kg)
\(\left[ {110;115} \right)\)
\(\left[ {115;120} \right)\)
\(\left[ {120;125} \right)\)
\(\left[ {125;130} \right)\)
Tần số
8
15
17
10
a) Đọc và giải thích dữ liệu cho bởi bảng tần số ghép nhóm trên.
b) Lập bảng tần số tương đối ghép nhóm.
Bảng tần số ghép nhóm sau cho biết cân nặng của một số con voi khi vừa sinh ra (đơn vị tính là kg ):
|
Cân nặng (kg) |
\(\left[ {110;115} \right)\) |
\(\left[ {115;120} \right)\) |
\(\left[ {120;125} \right)\) |
\(\left[ {125;130} \right)\) |
|
Tần số |
8 |
15 |
17 |
10 |
a) Đọc và giải thích dữ liệu cho bởi bảng tần số ghép nhóm trên.
b) Lập bảng tần số tương đối ghép nhóm.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Khi mới sinh, có 8 con voi có cân nặng từ 110 kg đến dưới \(115\;{\rm{kg}};15\) con có cân nặng từ 115 kg đến dưới \(120\;{\rm{kg}};17\) con có cân nặng từ 120 kg đến dưới \(125\;{\rm{kg}};10\) con có cân nặng từ 125 kg đến dưới 130 kg .
b) Tổng số con voi là \(n = 8 + 15 + 17 + 10 = 50\). Các tần số tương đối tương ứng là:
\(\frac{8}{{50}}.100\% = 16\% ;\frac{{15}}{{50}}.100\% = 30\% ;\frac{{17}}{{50}}.100\% = 34\% ;\frac{{10}}{{50}}.100\% = 20\% \)
Ta có bảng tần số tương đối ghép nhóm sau:
|
Cân nặng (kg) |
\(\left[ {110;115} \right)\) |
\(\left[ {115;120} \right)\) |
\(\left[ {120;125} \right)\) |
\(\left[ {125;130} \right)\) |
|
Tần số tương đối |
16% |
30% |
34% |
20% |
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Có 8 nhân viên của công ty đi làm hết dưới 15 phút; 15 nhân viên đi làm hết từ 15 phút đến dưới 30 phút; 12 nhân viên đi làm hết từ 30 phút đến dưới 45 phút; 5 nhân viên đi làm hết từ 45 phút đến dưới 60 phút.
Ta có bảng tần số ghép nhóm sau:
|
Thời gian (phút) |
\(\left[ {0;15} \right)\) |
\(\left[ {15;30} \right)\) |
\(\left[ {30;45} \right)\) |
\(\left[ {45;60} \right)\) |
|
Tần số |
8 |
15 |
12 |
5 |
b) Số nhân viên của công ty là \(n = 40\). Các tần số tương đối tương ứng là:
\({f_1} = \frac{8}{{40}}.100\% = 20\% ;{f_2} = \frac{{15}}{{40}}.100\% = 37,5\% \);\({f_3} = \frac{{12}}{{40}}.100\% = 30\% ;{f_4} = \frac{5}{{40}}.100\% = 12,5\% \)
Ta có bảng tần số tương đối ghép nhóm sau:
|
Thời gian (phút) |
\(\left[ {0;15} \right)\) |
\(\left[ {15;30} \right)\) |
\(\left[ {30;45} \right)\) |
\(\left[ {45;60} \right)\) |
|
Tần số tương đối |
\(20{\rm{\% }}\) |
\(37,5{\rm{\% }}\) |
\(30{\rm{\% }}\) |
\(12,5{\rm{\% }}\) |
Lời giải
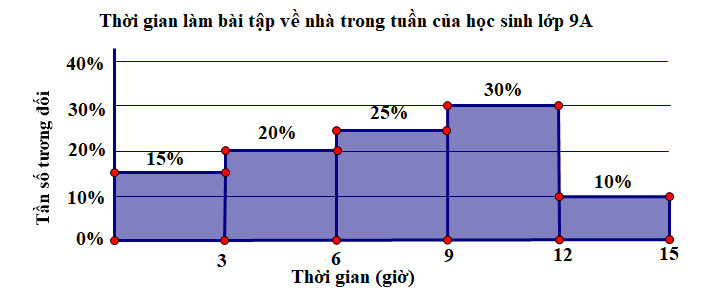
a) Tỉ lệ học sinh trong lớp dành ít nhất 6 giờ trong tuần để làm bài tập về nhà là:\(25\% + 30\% + 10\% = 65\% {\rm{. }}\)
b) Số học sinh lớp 9 A dành ít nhất 6 giờ trong tuần để làm bài tập về nhà là:\(40 \cdot 65\% = 26\) (học sinh).
c) Biểu đồ tần số tương đối ghép nhóm dạng cột:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập