Mẫu số liệu dưới đây ghi lại tốc độ (đơn vị: \(\left[ {40;70} \right)\) ) của \(44\) ô tô khi đi qua một trạm đo tốc độ:
\[\begin{array}{*{20}{l}}{48,5}&{43}&{50}&{55}&{45}&{60}&{53}&{55,5}&{44}&{65}&{54,5}\\{51}&{62,5}&{41}&{44,5}&{57}&{57}&{68}&{49}&{46,5}&{53,5}&{49}\\{61}&{49,5}&{54}&{62}&{59}&{56}&{47}&{50}&{59,5}&{61}&{46,5}\\{49,5}&{52,5}&{57}&{47}&{59}&{55}&{45}&{47,5}&{48}&{61,5}&{48,5}\end{array}\]
Hãy ghép các số liệu thành sáu nhóm ứng với sáu nửa khoảng có độ dài bằng nhau?
Mẫu số liệu dưới đây ghi lại tốc độ (đơn vị: \(\left[ {40;70} \right)\) ) của \(44\) ô tô khi đi qua một trạm đo tốc độ:
\[\begin{array}{*{20}{l}}{48,5}&{43}&{50}&{55}&{45}&{60}&{53}&{55,5}&{44}&{65}&{54,5}\\{51}&{62,5}&{41}&{44,5}&{57}&{57}&{68}&{49}&{46,5}&{53,5}&{49}\\{61}&{49,5}&{54}&{62}&{59}&{56}&{47}&{50}&{59,5}&{61}&{46,5}\\{49,5}&{52,5}&{57}&{47}&{59}&{55}&{45}&{47,5}&{48}&{61,5}&{48,5}\end{array}\]
Hãy ghép các số liệu thành sáu nhóm ứng với sáu nửa khoảng có độ dài bằng nhau?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Trong mẫu số liệu đó, số liệu có giá trị nhỏ nhất là \[41\], số liệu có giá trị lớn nhất là \[68\]. Vì thế, ta có thể chọn nửa khoảng \(\left[ {40;70} \right)\) sao cho giá trị của mỗi số liệu trong mẫu số liệu đều thuộc nửa khoảng \(\left[ {40;70} \right)\). Vì độ dài của nửa khoảng \(\left[ {40;70} \right)\) bằng \(70 - 40 = 30\) nên ta có thể phân chia nửa khoảng đó thành sáu nửa khoảng có độ dài bằng nhau là: \(\left[ {40;45} \right)\), \(\left[ {45;50} \right),\left[ {50;55} \right),\left[ {55;60} \right)\), \[\left[ {60;65} \right),\] \(\left[ {65;70} \right)\).
Vậy ta có thể ghép nhóm mẫu số liệu đã cho theo sáu nhóm ứng vởi sáu nửa khoảng đó.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Có 8 nhân viên của công ty đi làm hết dưới 15 phút; 15 nhân viên đi làm hết từ 15 phút đến dưới 30 phút; 12 nhân viên đi làm hết từ 30 phút đến dưới 45 phút; 5 nhân viên đi làm hết từ 45 phút đến dưới 60 phút.
Ta có bảng tần số ghép nhóm sau:
|
Thời gian (phút) |
\(\left[ {0;15} \right)\) |
\(\left[ {15;30} \right)\) |
\(\left[ {30;45} \right)\) |
\(\left[ {45;60} \right)\) |
|
Tần số |
8 |
15 |
12 |
5 |
b) Số nhân viên của công ty là \(n = 40\). Các tần số tương đối tương ứng là:
\({f_1} = \frac{8}{{40}}.100\% = 20\% ;{f_2} = \frac{{15}}{{40}}.100\% = 37,5\% \);\({f_3} = \frac{{12}}{{40}}.100\% = 30\% ;{f_4} = \frac{5}{{40}}.100\% = 12,5\% \)
Ta có bảng tần số tương đối ghép nhóm sau:
|
Thời gian (phút) |
\(\left[ {0;15} \right)\) |
\(\left[ {15;30} \right)\) |
\(\left[ {30;45} \right)\) |
\(\left[ {45;60} \right)\) |
|
Tần số tương đối |
\(20{\rm{\% }}\) |
\(37,5{\rm{\% }}\) |
\(30{\rm{\% }}\) |
\(12,5{\rm{\% }}\) |
Lời giải
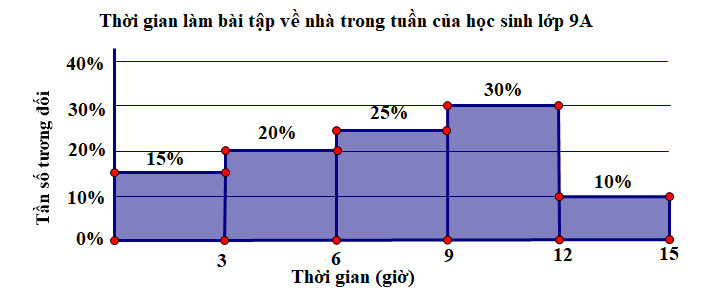
a) Tỉ lệ học sinh trong lớp dành ít nhất 6 giờ trong tuần để làm bài tập về nhà là:\(25\% + 30\% + 10\% = 65\% {\rm{. }}\)
b) Số học sinh lớp 9 A dành ít nhất 6 giờ trong tuần để làm bài tập về nhà là:\(40 \cdot 65\% = 26\) (học sinh).
c) Biểu đồ tần số tương đối ghép nhóm dạng cột:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập