Cho đoạn thẳng \[AB = 8\] cm. Trên tia \[AB\] lấy điểm \[C\] sao cho \[AC = 4\] cm.
a) Điểm \[C\] có nằm giữa hai điểm \[A\] và \[B\] không? Vì sao?
b) Tính độ dài đoạn \[BC\].
c) Điểm \[C\] có là trung điểm của đoạn thẳng \[AB\] không? Vì sao?
Cho đoạn thẳng \[AB = 8\] cm. Trên tia \[AB\] lấy điểm \[C\] sao cho \[AC = 4\] cm.
a) Điểm \[C\] có nằm giữa hai điểm \[A\] và \[B\] không? Vì sao?
b) Tính độ dài đoạn \[BC\].
c) Điểm \[C\] có là trung điểm của đoạn thẳng \[AB\] không? Vì sao?
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 6 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
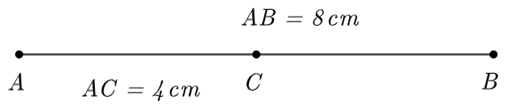
a) Ta có điểm \[C\] nằm trên đoạn thẳng \[AB\].
Mà \[AC < AB\] (vì \[AC = 4\] cm, \[AB = 8\] cm).
Do đó điểm \[C\] nằm giữa hai điểm \[A\] và \[B\].
b) Vì điểm \[C\] nằm giữa hai điểm \[A\] và \[B\] nên:
\[AC + BC = AB\]
\[4 + BC = 8\]
Suy ra \[BC = 8--4 = 4\] (cm)
Vậy \[BC = 4\] cm.
c) Điểm \[C\] là trung điểm của đoạn thẳng \[AB\] vì:
• Điểm \[C\] nằm giữa hai điểm \[A\] và \[B\].
• \[AC = BC{\rm{ }}( = 4\] cm).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có: \[A = \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + ... + \frac{1}{{2022}}\];
\[B = \frac{{2021}}{1} + \frac{{2020}}{2} + \frac{{2019}}{3} + ... + \frac{1}{{2021}}\]
\[ = 2021 + \frac{{2020}}{2} + \frac{{2019}}{3} + ... + \frac{1}{{2021}}\]
\[ = 2020 + \frac{{2020}}{2} + \frac{{2019}}{3} + ... + \frac{1}{{2021}} + 1\]
\[ = \,\left( {1 + \frac{{2020}}{2}} \right) + \left( {1 + \frac{{2019}}{3}} \right) + ... + \left( {\frac{1}{{2021}} + 1} \right) + 1\]
\[ = \,\frac{{2022}}{2} + \frac{{2022}}{3} + ... + \frac{{2022}}{{2021}} + \frac{{2022}}{{2022}}\]
\[ = 2022\,\,.\,\,\left( {\frac{1}{2} + \frac{1}{3} + ... + \frac{1}{{2021}} + \frac{1}{{2022}}} \right)\].
Khi đó, \[\frac{B}{A} = \frac{{2022\,\,.\,\,\left( {\frac{1}{2} + \frac{1}{3} + ... + \frac{1}{{2021}} + \frac{1}{{2022}}} \right)}}{{\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + ... + \frac{1}{{2022}}}} = 2022\].
Vậy tỉ số \[\frac{B}{A} = 2022\].
Lời giải
a) Vì chiều dài của đám đất hình chứ nhật bằng \[\frac{4}{3}\] chiều rộng
Suy ra, chiều rộng đám đất là: \[80:\frac{4}{3} = 60\] (m)
Diện tích đám đất hình chữ nhật là: \[80\,\,.\,\,60\, = 4{\rm{ }}800\] (m2).
Vậy diện tích của đám đất là \[4{\rm{ }}800\] m2.
b) Vì \[\frac{5}{8}\] diện tích đám đất đó được dùng để trồng cây.
Nên diện tích dùng để trồng cây là: \[4{\rm{ }}800\,.\,\,\frac{5}{8} = 3{\rm{ }}000\] (m2)
Phần diện tích còn lại của đám đất sau khi trồng cây là:
\[4{\rm{ }}800 - 3{\rm{ }}000 = 1{\rm{ }}800\] (m2)
Vì \[40\% \] diện tích còn lại dùng để đào ao thả cá nên phần diện tích đất để đào ao thả cá là:
\(\frac{{1\,\,800\,.\,40}}{{100}} = 720\) (m2).
Vậy diện tích ao cá là 720 m2.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.