Một hộp đựng mỹ phẩm được thiết kế (tham khảo hình vẽ) có thân hộp là hình trụ có bán kính hình tròn đáy \(r = 5cm\), chiều cao \(h = 6cm\)và nắp hộp là một nửa hình cầu. Người ta cần sơn mặt ngoài của cái hộp đó (không sơn đáy) thì diện tích \(S\)cần sơn là bao nhiêu?
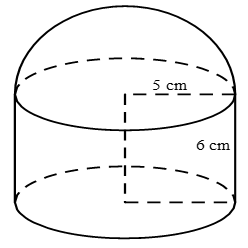
Một hộp đựng mỹ phẩm được thiết kế (tham khảo hình vẽ) có thân hộp là hình trụ có bán kính hình tròn đáy \(r = 5cm\), chiều cao \(h = 6cm\)và nắp hộp là một nửa hình cầu. Người ta cần sơn mặt ngoài của cái hộp đó (không sơn đáy) thì diện tích \(S\)cần sơn là bao nhiêu?

Quảng cáo
Trả lời:
Diện tích nắp hộp cần sơn là: \({S_1} = \frac{{4\pi {r^2}}}{2} = 50\pi \)\(c{m^2}\).
Diện tích than hộp cần sơn là: \({S_2} = 2\pi rh = 60\pi \)\(c{m^2}\).
Diện tích \(S\)cần sơn là: \(S = {S_1} + {S_2} = 50\pi + 60\pi = 110\pi \)\(c{m^2}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Vì Trái Đất hình cầu có bán kính R = 6370 km nên diện tích bề mặt Trái Đất là:
Sbề mặt = 4pR2
= 4. 3,14. 63702
= 509.645.864 (km2)
Vậy diện tích bề mặt Trái Đất bị bao phủ bởi nước là (100% – 29%). 509.645.864 = 361.848.563 (km2)
Lời giải
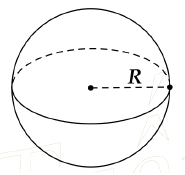
Vì quả pha lê hình cầu có diện tích Smặt cầu = 144p cm2 nên:
\[\begin{array}{l}S = 4\pi {R^2}\\{R^2} = \frac{S}{{4\pi }}\\{R^2} = \frac{{144\pi }}{{4\pi }}\\{R^2} = 36\\ \Rightarrow R = 6\left( {cm} \right)\end{array}\]
Vậy thể tích quả pha lê là: \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {.6^3} = 228\pi \)cm3.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.