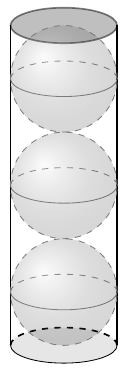
Một tháp nước có bể chứa hình cầu, đường kính bên trong của bể đo được là 6 m.
a) Tính thể tích của tháp nước đó?
b) Biết rằng lượng nước đựng đầu trong bể đủ dùng cho một khu dân cư trong 5 ngày. Cho biết khu dân cư có 1304 người. Hỏi trong một ngày mức bình quân mỗi người dùng bao nhiêu lít nước (lấy p = 3,14; biết 1 m3 = 1000 lít).

Một tháp nước có bể chứa hình cầu, đường kính bên trong của bể đo được là 6 m.
a) Tính thể tích của tháp nước đó?
b) Biết rằng lượng nước đựng đầu trong bể đủ dùng cho một khu dân cư trong 5 ngày. Cho biết khu dân cư có 1304 người. Hỏi trong một ngày mức bình quân mỗi người dùng bao nhiêu lít nước (lấy p = 3,14; biết 1 m3 = 1000 lít).

Quảng cáo
Trả lời:
a) Vì tháp nước hình cầu có R = 6 : 2 = 3 m nên thể tích của tháp nước là:
\[V = \frac{4}{3}\pi {R^3} = 4.3,{14.3^2} = 113,04\left( {{m^3}} \right) = 113040\left( {lit} \right)\]
Vậy thể tích của tháp nước là 113040 lít.
b) Một ngày khu dân cư dùng hết số nước là: \[113040:5 = 22608\left( {lit} \right)\]
Vậy trong một ngày mức bình quân mỗi người dùng 22608 : 1304 = 13,34 lít.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
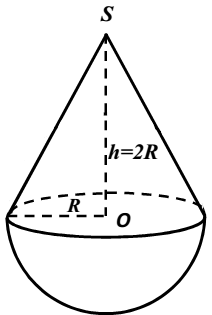
Thể tích hình nón là \[{V_1} = \frac{1}{3}\pi .{R^2}.2R = \frac{2}{3}\pi .{R^3}\]
Thể tích nửa hình cầu là \({V_2} = \frac{1}{2}.\frac{4}{3}\pi .{R^3} = \frac{2}{3}\pi .{R^3}\)
Thể tích của toàn bộ khối đồ vật là:
\({V_1} + {V_2} = 36\pi \)
\(\begin{array}{l}\frac{4}{3}\pi .{R^3} = 36\pi \\ \Rightarrow R = 3\end{array}\)
Diện tích xung quanh của mặt nón là \({S_1} = \pi R.\sqrt {4{R^2} + {R^2}} = \pi {R^2}\sqrt 5 = 9\sqrt 5 \pi \)
Diện tích của nửa mặt cầu là \({S_2} = \frac{1}{2}.4\pi {R^2} = 18\pi \)
Diện tích bề mặt của toàn bộ đồ vật bằng \({S_1} + {S_2} = 9\pi \left( {\sqrt 5 + 2} \right){\rm{ }}c{m^2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.



![Người ta thả một viên bi có dạng hình cầu có bán kính \[2,7\,cm\] vào một chiếc cốc hình trụ đang chứa nước (tham khảo hình vẽ dưới). Biết rằng bán kính của phần trong đáy cốc bằng \[5,4\,cm\] và chiều cao của mực nước ban đầu trong cốc bằng \[4,5\,cm\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/16-1769749596.png)