Công ty vàng bạc đá quý muốn làm một món đồ trang sức có hình hai hình cầu bằng nhau giao nhau như hình vẽ. Khối cầu có bán kính \[25cm\]khoảng cách giữa hai tâm hình cầu là \[40cm\]. Giá mạ vàng \[1{m^2}\] là \[470.000\]đồng. Nhà sản xuất muốn mạ vàng xung quanh món đồ trang sức đó. Tính số tiền cần dùng để mạ vàng khối trang sức đó.
![Công ty vàng bạc đá quý muốn làm một món đồ trang sức có hình hai hình cầu bằng nhau giao nhau như hình vẽ. Khối cầu có bán kính \[25cm\]khoảng cách giữa hai tâm hình cầu là \[40cm\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/21-1769749708.jpg)
Công ty vàng bạc đá quý muốn làm một món đồ trang sức có hình hai hình cầu bằng nhau giao nhau như hình vẽ. Khối cầu có bán kính \[25cm\]khoảng cách giữa hai tâm hình cầu là \[40cm\]. Giá mạ vàng \[1{m^2}\] là \[470.000\]đồng. Nhà sản xuất muốn mạ vàng xung quanh món đồ trang sức đó. Tính số tiền cần dùng để mạ vàng khối trang sức đó.
![Công ty vàng bạc đá quý muốn làm một món đồ trang sức có hình hai hình cầu bằng nhau giao nhau như hình vẽ. Khối cầu có bán kính \[25cm\]khoảng cách giữa hai tâm hình cầu là \[40cm\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/21-1769749708.jpg)
Quảng cáo
Trả lời:
![Công ty vàng bạc đá quý muốn làm một món đồ trang sức có hình hai hình cầu bằng nhau giao nhau như hình vẽ. Khối cầu có bán kính \[25cm\]khoảng cách giữa hai tâm hình cầu là \[40cm\] (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2026/01/screenshot-5579-1769749747.png)
(Phần màu nhạt là phần giao nhau của hai khối cầu)
Gọi h là chiều cao của chỏm cầu. Ta có \[h = \frac{{2R - d}}{2} = \frac{{2.25 - 40}}{2} = 5cm\]
(\[d\]là khoảng cách giữa hai tâm)
Diện tích xung quanh của chỏm cầu là:\[{S_{xq}} = 2\pi Rh\]
Vì 2 khối cầu bằng nhau nên 2 hình chỏm cầu bằng nhau.
\[{S_{xq}}\] khối trang sức \[ = 2{S_{xq}}\] khối cầu\[ - 2{S_{xq}}\] chỏm cầu.
Khối trang sức có \[{S_{xq}} = 2.4\pi {R^2} - 2.2\pi Rh = 2.4\pi {.25^2} - 2.2\pi .25.5 = 4500\pi c{m^2} = 0.45{m^2}\]
Vậy số tiền dùng để mạ vàng khối trang sức đó là \[470.000.0,45\pi \simeq 664.000\]đồng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
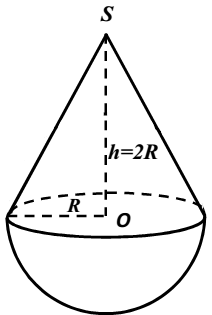
Thể tích hình nón là \[{V_1} = \frac{1}{3}\pi .{R^2}.2R = \frac{2}{3}\pi .{R^3}\]
Thể tích nửa hình cầu là \({V_2} = \frac{1}{2}.\frac{4}{3}\pi .{R^3} = \frac{2}{3}\pi .{R^3}\)
Thể tích của toàn bộ khối đồ vật là:
\({V_1} + {V_2} = 36\pi \)
\(\begin{array}{l}\frac{4}{3}\pi .{R^3} = 36\pi \\ \Rightarrow R = 3\end{array}\)
Diện tích xung quanh của mặt nón là \({S_1} = \pi R.\sqrt {4{R^2} + {R^2}} = \pi {R^2}\sqrt 5 = 9\sqrt 5 \pi \)
Diện tích của nửa mặt cầu là \({S_2} = \frac{1}{2}.4\pi {R^2} = 18\pi \)
Diện tích bề mặt của toàn bộ đồ vật bằng \({S_1} + {S_2} = 9\pi \left( {\sqrt 5 + 2} \right){\rm{ }}c{m^2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.



![Người ta thả một viên bi có dạng hình cầu có bán kính \[2,7\,cm\] vào một chiếc cốc hình trụ đang chứa nước (tham khảo hình vẽ dưới). Biết rằng bán kính của phần trong đáy cốc bằng \[5,4\,cm\] và chiều cao của mực nước ban đầu trong cốc bằng \[4,5\,cm\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/16-1769749596.png)