Cho tam giác \(ABC\) vuông tại \(A,BC = 10\;{\rm{cm}}\), đường cao \(AH = 4\;{\rm{cm}}\). Quay tam giác \(ABC\) một vòng quanh cạnh \(BC\). Tính thể tích hình tạo thành.
Cho tam giác \(ABC\) vuông tại \(A,BC = 10\;{\rm{cm}}\), đường cao \(AH = 4\;{\rm{cm}}\). Quay tam giác \(ABC\) một vòng quanh cạnh \(BC\). Tính thể tích hình tạo thành.
Quảng cáo
Trả lời:
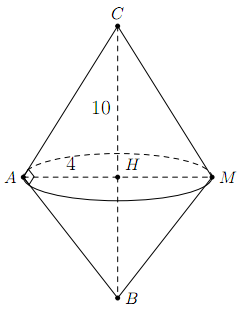
Khi quay tam giác \(ABC\) một vòng quanh cạnh \(BC\), hình tạo thành gồm hai hình nón có đường cao theo thứ tự là \(HB\) và \(HC\). Thể tích của hình tạo thành bằng.
\(\frac{1}{3}\pi \cdot A{H^2} \cdot BH + \frac{1}{3}\pi \cdot A{H^2} \cdot CH = \frac{1}{3}\pi \cdot A{H^2}(BH + CH)\)
\( = \frac{1}{3}\pi \cdot A{H^2}.BC = \frac{1}{3}\pi \cdot {4^2}.10 = \frac{{160}}{3}\pi \,\,(c{m^3})\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi bán kính đáy thùng rác văn phòng là \(R\) và chiều cao \(h.\)
Theo đề bài, ta có: \(R = \frac{{0,4}}{2} = 0,2{\rm{m; }}h = 0,8{\rm{m}}{\rm{.}}\)
Thể tích thùng rác: \(V = \pi {R^2}h = \pi {\left( {0,2} \right)^2}.0,8 = \frac{4}{{125}}\pi \left( {{{\rm{m}}^{\rm{3}}}} \right).\)
Lời giải
Bán kính hình trụ bên trong là: \(r = 1 - 0,05 = 0,95\left( {\rm{m}} \right).\)
Áp dụng công thức tính thể tích hình trụ, ta có: \(V = \pi {r^2}h = \pi {\left( {0,95} \right)^2}.1,5 \approx 4,25\left( {{{\rm{m}}^{\rm{3}}}} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.


![Tính lượng vải cần mua để tạo ra nón của chú Hề trong hình bên. Biết rằng tỉ lệ khấu hao vải khi may nón là \[{\rm{15}}\% .\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/18-1769751657.png)