Cho tam giác đều ABC nội tiếp đường tròn \(({\rm{O}})\) như hình vẽ. Phép quay ngược chiều 60o tâm O biến các điểm \(A,B,C\) lần lượt thành các điểm \(D,E,F\). Chứng minh rằng \[ADBECF\] là một lục giác đều.
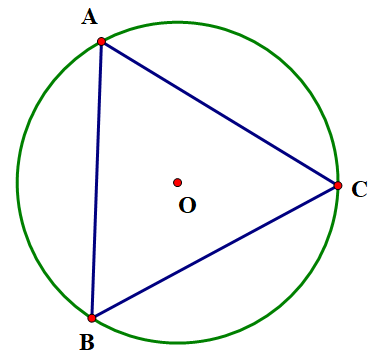
Cho tam giác đều ABC nội tiếp đường tròn \(({\rm{O}})\) như hình vẽ. Phép quay ngược chiều 60o tâm O biến các điểm \(A,B,C\) lần lượt thành các điểm \(D,E,F\). Chứng minh rằng \[ADBECF\] là một lục giác đều.

Câu hỏi trong đề: 18 bài tập Toán 9 Cánh diều Ôn tập chương 9 có đáp án !!
Quảng cáo
Trả lời:
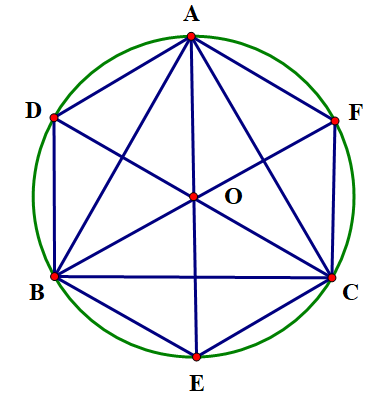
Phép quay ngược chiều 60o tâm O biến A thành D. Ta có: \(OD = OA\) và nên tam giác \(AOD\) là tam giác đều \[ \Rightarrow AD = OA = OD = R\] (R là bán kính đường tròn \(\left( O \right)\)).
Chứng minh tương tự, ta có: \(BE = CF = R\)\( \Rightarrow AD = BE = CF = R(*)\)
Tam giác \(ABC\) đều nội tiếp đường tròn \(\left( {\rm{O}} \right)\), ta có: \({\rm{OD}} = {\rm{OA}} = {\rm{OB}}\) (1)
Lại có mà (cmt)
Từ (1) và (2) suy ra tam giác \(DOB\) là tam giác đều.
Chứng minh tương tự các tam giác \(EOC\) và \(FOA\) cũng là tam giác đều.\( \Rightarrow DB = EC = EA = R\left( {**} \right)\)
Từ (*) và (**)\( \Rightarrow AD = DB = BE = EC = CE = EA\left( { = R} \right)\left( 3 \right)\)
Dễ thấy \(\widehat {{\rm{ADB}}} = \widehat {{\rm{DBE}}} = \widehat {{\rm{BEC}}} = \widehat {{\rm{ECF}}} = \widehat {{\rm{CFA}}} = \widehat {{\rm{FAD}}}\) (4)
Từ (3) và \((4) \Rightarrow ADBECF\) là một lục giác đều.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
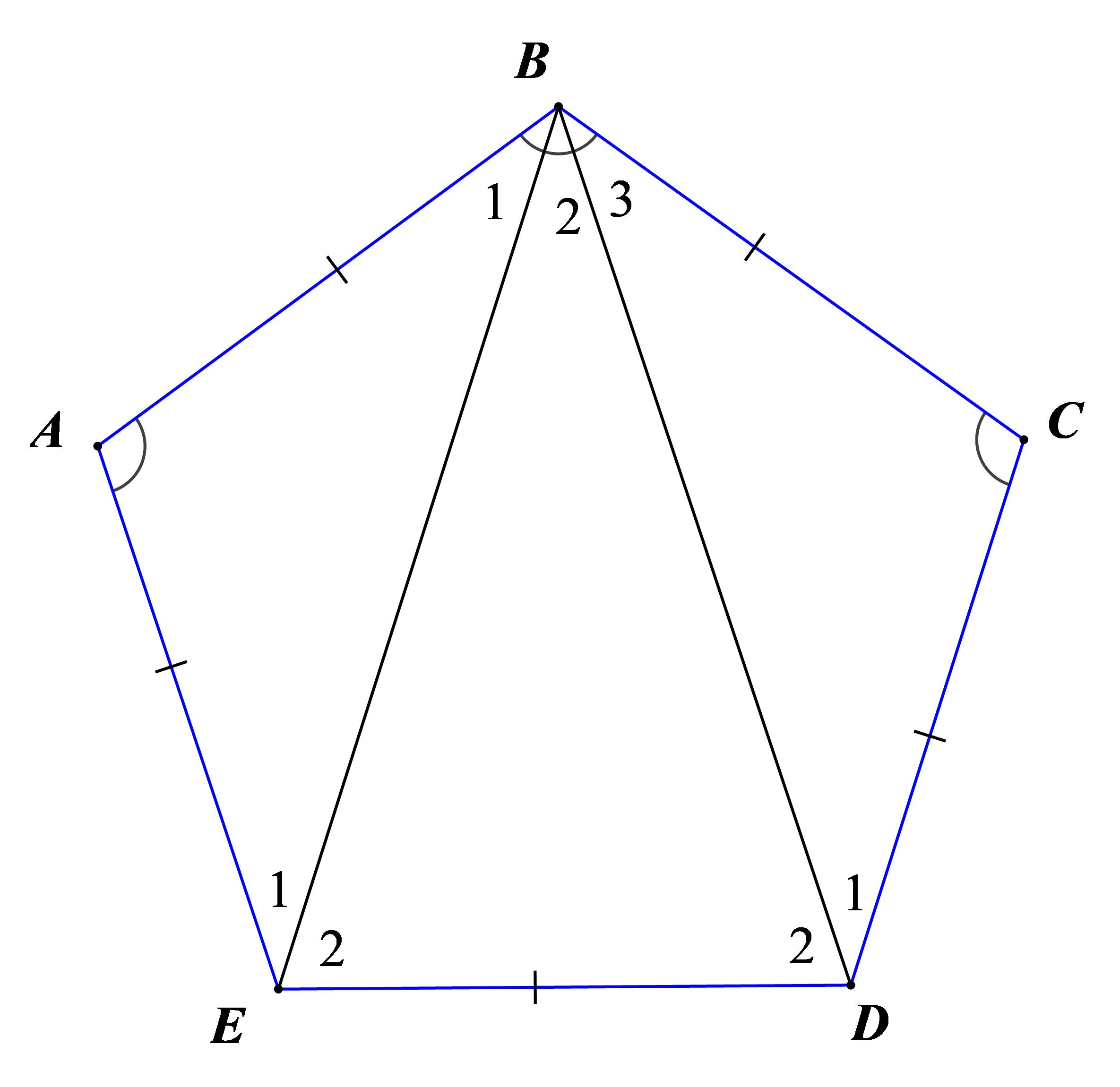
Ta có : \(AB = BC = CD = DE = EA\,\,\left( {gt} \right)\,\,\left( * \right)\)
Xét tam giác \(ABE\) có \(AB = AE\,\,\) (gt)
Nên \(\Delta ABE\) cân tại A có \(\widehat A = 108^\circ \)
\( \Rightarrow {\widehat B_1} = {\widehat E_1} = \frac{{180^\circ - \widehat A}}{2} = \frac{{180^\circ - 108^\circ }}{2} = 36^\circ \)
Tương tự với tam giác \(BCD\), ta có : \({\widehat B_3} = {\widehat D_1} = 36^\circ \)
Lại có \(\widehat {ABC} = {\widehat B_1} + {\widehat B_2} + {\widehat B_3} = 108^\circ \)
\( \Rightarrow {\widehat B_2} = 108^\circ - \left( {{{\widehat B}_1} + {{\widehat B}_3}} \right) = 108^\circ - \left( {36^\circ + 36^\circ } \right) = 36^\circ \)
Dễ thấy \(\Delta ABE = \Delta CBD\,\,\left( {c.g.c} \right)\)
Lời giải
a) Phép quay ngược chiều 72o tâm O biến điểm A biến B thì các điểm \(B,C,D,E\) lần lượt biến thành các điểm \(C,D,E\)và A .
b) Ba phép quay tâm O giữ nguyên hình ngũ giác đều:
1. Phép quay ngược chiều 144o;
2. Phép quay ngược chiều 216o;
3. Phép quay thuận chiều 72o.
Bạn hãy tìm thêm những phép quay còn lại giữ nguyên hình ngũ giác đều.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hình ngũ giác đều \[ABCDE\]có tâm \(O\) (Hình vẽ). a) Phép quay ngược chiều tâm O biến điểm A thành điểm B thì các điểm \(B,C,D,E\) tương ứng biến thành các điểm nào? b) Chỉ ra ba phép quay tâm O giữ nguyên hình ngũ giác đều đã cho. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/19-1769711285.png)