Một trái dưa có dạng hình cầu. Bổ đôi trái dưa này ra thì mặt cắt có diện tích là \(314\;{\rm{c}}{{\rm{m}}^2}\). Tính thể tích của trái dưa đó.
Một trái dưa có dạng hình cầu. Bổ đôi trái dưa này ra thì mặt cắt có diện tích là \(314\;{\rm{c}}{{\rm{m}}^2}\). Tính thể tích của trái dưa đó.
Quảng cáo
Trả lời:
Khi bổ đôi trái dưa thì mặt cắt là một hình tròn. Ta có: \(S = \pi {R^2} \Rightarrow R = \sqrt {\frac{S}{\pi }} \approx \sqrt {\frac{{314}}{{3,14}}} = 10\;{\rm{cm}}\)
Vậy bán kính của trái dưa là \(10\;{\rm{cm}}\). Thể tích của trái dưa là:
\(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi \cdot {10^3} \approx 4187\;{\rm{c}}{{\rm{m}}^3}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
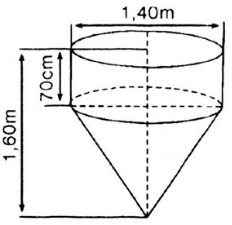
Bán kính hình trụ bên trong là: \(r = 1 - 0,05 = 0,95\left( {\rm{m}} \right).\)
Áp dụng công thức tính thể tích hình trụ, ta có: \(V = \pi {r^2}h = \pi {\left( {0,95} \right)^2}.1,5 \approx 4,25\left( {{{\rm{m}}^{\rm{3}}}} \right).\)
Lời giải
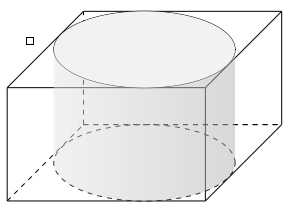
Gọi bán kính và chiều cao của hình trụ lần lượt là \(R\) và \(h\).
Khi đó hình hộp chữ nhật có cạnh đáy là \[2R\] và chiều cao là\[h\]. Gọi \({V_1}\) và \({V_2}\) lần lượt là thể tích của hình trụ và hình hộp.
Ta có \(\frac{{{V_1}}}{{{V_2}}} = \frac{{\pi {R^2}h}}{{4{R^2}h}}.\) Do đó \(\frac{{270}}{{{V_2}}} = \frac{\pi }{4}\).
Suy ra \({V_2} = \frac{{270 \cdot 4}}{\pi } \approx 344\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\)
Vậy thể tích hình hộp là \(344\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.