Cho đường thẳng \[xy\]. Trên đường thẳng \[xy\] lấy điểm \(O\). Lấy điểm \[A\] thuộc tia \[Ox\] sao cho \[OA = 4\] cm, điểm \[B\] thuộc tia \[Oy\] sao cho \[OB = 2\] cm.
a) Trong ba điểm \(A,O,B\) thì điểm nào nằm giữa hai điểm còn lại? Tính \(AB\).
b) Gọi \(I\) là trung điểm \[OA\], điểm \[O\] có là trung điểm của \[IB\] không? Tại sao?
Cho đường thẳng \[xy\]. Trên đường thẳng \[xy\] lấy điểm \(O\). Lấy điểm \[A\] thuộc tia \[Ox\] sao cho \[OA = 4\] cm, điểm \[B\] thuộc tia \[Oy\] sao cho \[OB = 2\] cm.
a) Trong ba điểm \(A,O,B\) thì điểm nào nằm giữa hai điểm còn lại? Tính \(AB\).
b) Gọi \(I\) là trung điểm \[OA\], điểm \[O\] có là trung điểm của \[IB\] không? Tại sao?
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 6 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
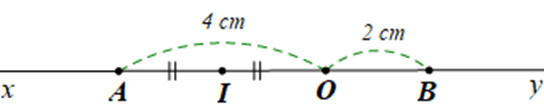
a) Vì \(OA\) và \(OB\) là hai tia đối nhau nên \(O\) nằm giữa \(A\) và \(B\).
Do đó \[AB = OA + OB = 4 + 2 = 6\] (cm).
b) Vì \(I\) là trung điểm của \[OA\] nên \[OI = \frac{1}{2}OA = \frac{1}{2}\,\,.\,\,4 = 2\] (cm).
Vì \[I\] thuộc tia \[Ox\] nên \[OI\] và \[OB\] là hai tia đối nhau.
Mà \[OI = OB\] (cùng bằng 2 cm).
Suy ra \[I\] là trung điểm của \[OB\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Ta có \[A = \frac{{2n - 1}}{{3 - n}}\]\[ = \frac{{2n - 6 + 5}}{{\left( { - 1} \right)\left( {n - 3} \right)}}\]\[ = - \frac{{2\left( {n - 3} \right) + 5}}{{n - 3}}\]\[ = - \frac{{2\left( {n - 3} \right)}}{{n - 3}} - \frac{5}{{n - 3}}\].
Vì \[2\left( {n--3} \right)\,\, \vdots \,\,\left( {n--3} \right)\] nên để biểu thức \[A\] có giá trị là một số nguyên thì \[5\,\, \vdots \,\,\left( {n--3} \right).\] Suy ra: \[\left( {n--3} \right) \in \] Ư\[(5) = \left\{ {--\,5\,;\,\,--\,\,1\,;\,\,1\,;\,\,5} \right\}\].
Ta có bảng sau:
|
\[n--3\] |
\[--\,5\] |
\[--\,1\] |
1 |
5 |
|
\[n\] |
\[--\,2\] |
2 |
4 |
8 |
Vì \[n\] là số nguyên cho nên tất cả các giá trị \[n\] tìm được ở bảng trên đều thỏa mãn.
Vậy để biểu thức \[A\] có giá trị nguyên thì \[n \in \left\{ {--\,2\,;\,\,2\,;\,\,4\,;\,\,8} \right\}\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Phân số chỉ số trang sách đọc trong ngày thứ ba là:
\(1 - \left( {\frac{2}{5} + \frac{7}{{15}}} \right) = \frac{2}{{15}}\) (số trang của cuốn sách)
Số trang của cuốn sách là: \(20:\frac{2}{{15}} = 150\) (trang).
Vậy số trang của cuốn sách là 150 (trang).
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập