Cho \(x\) thoả mãn: \[x + \frac{7}{3} = \frac{{ - 5}}{2}\]. Khi đó, giá trị của \(x\) bằng
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 6 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: A
\[x + \frac{7}{3} = \frac{{ - 5}}{2}\]
\[x = \frac{{ - 5}}{2} - \frac{7}{3}\]
\[x = \frac{{ - 29}}{6}\]
Vậy \[x = \frac{{ - 29}}{6}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
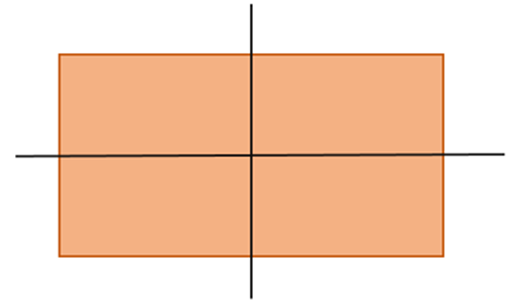
1. • Hình chữ nhật có hai trục đối xứng chia hình chữ nhật thành hai phần (như hình vẽ).
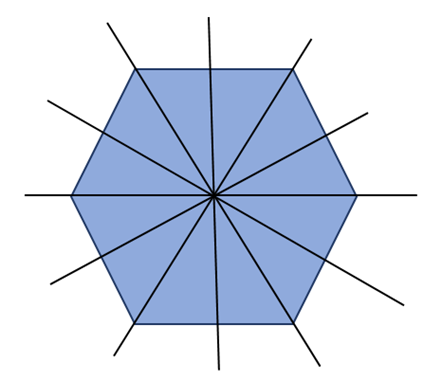
• Hình lục giác đều có 6 trục đối xứng là các đường thẳng lần lượt chia hình lục giác thành hai nửa (như hình vẽ).
2.
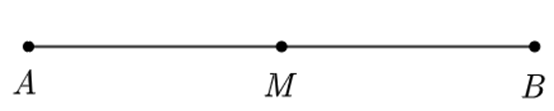
a) Theo đề bài ta có hai điểm \[M\] và \[B\] thuộc tia \[AB\].
Mà độ dài đoạn thẳng \[AB = 6\] cm và \[AM = 3\] cm, suy ra \[AM < AB\].
Vậy điểm \[M\] nằm giữa hai điểm \[A\] và \[B\].
b) Vì điểm \[M\] nằm giữa hai điểm \[A\] và \[B\] nên:
\[AM + MB = AB\] với \[AB = 6\] cm và \[AM = 3\] cm;
Độ dài đoạn thẳng \[MB\] là: \[MB = AB--AM = 6--3 = 3\] (cm).
Suy ra: \[AM = MB = 3\] cm.
* Điểm \[M\] là trung điểm của đoạn thẳng \[AB\] vì:
• Điểm \[M\] nằm giữa hai điểm \[A\] và \[B\];
• \[AM = MB\].
Lời giải
a) Số trang sách bạn An đọc được trong ngày thứ nhất là:
\[120\,\,.\,\,\frac{2}{5} = 48\] (trang)
Vậy ngày thứ nhất bạn An đọc được 48 trang sách.
b) Sau ngày thứ nhất, số trang sách còn lại là:
\[120 - 48 = 72\] (trang);
Số trang sách ngày thứ hai bạn An đọc được là:
\[72\,\,.\,\,\frac{2}{3} = 48\] (trang);
Số trang sách bạn An đọc trong ngày thứ ba là:
\[72--48 = 24\] (trang).
Vậy trong ngày thứ ba bạn An đọc được 24 trang.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.