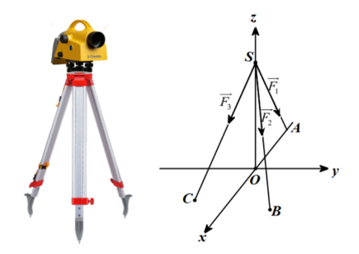
Một chiếc máy đo đạc trắc địa được đặt trên một giá đỡ ba chân với điểm đặt \(S\left( {0;0;4} \right)\) và các điểm tiếp xúc với mặt đất của ba chân lần lượt là \(A\left( { - 2;0;0} \right),\,\,B\left( {1;\sqrt 3 ;0} \right),\,\,C\left( {1; - \sqrt 3 ;0} \right)\). Biết rằng trọng lực tác dụng lên chiếc máy có độ lớn là \(24\,N\) và được phân bố thành ba lực   \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} ,\,\,\overrightarrow {{F_3}} \) có độ lớn bằng nhau như hình dưới. Tính tích vô hướng của \(\overrightarrow {{F_1}} .\overrightarrow {{F_2}} \).

Gọi biến cố A: “An làm đúng mỗi câu đề ôn tập ở mức độ dễ” \( \Rightarrow P(A) = 0,8\).

Biến cố B: “An làm đúng mỗi câu đề ôn tập ở mức độ trung bình” \( \Rightarrow P(B) = 0,6\).

Biến cố C: “An làm đúng mỗi câu đề ôn tập ở mức độ khó” \( \Rightarrow P(C) = 0,15\).

a) Sai. Xác suất để An làm ba câu thuộc ba loại và đúng cả ba câu là

\(P\left( {ABC} \right) = 0,8 \times 0,6 \times 0,15 = 0,072 = 7,2\% \).

b) Sai. Khi An làm 3 câu thuộc ba loại khác nhau. Xác suất để An làm đúng 2 trong số 3 câu là

\(P\left( {AB\overline C \cup A\overline B C \cup \overline A BC} \right) = 0,8 \times 0,6 \times 0,85 + 0,8 \times 0,4 \times 0,15 + 0,2 \times 0,6 \times 0,15 = 0,474\).

c) Đúng. Xác suất để An làm đúng 3 câu đủ ba loại là \(0,072\).

Xác suất để An làm sai 3 câu ở mức độ trung bình là \(0,4 \times 0,4 \times 0,4 = 0,064 < 0,072\).

Đáp án: 2550.

Giả sử ba tấm thẻ lấy ra có số ghi là \(a,b,c\) theo thứ tự tăng dần (\(a < b < c\)).

Để ba số này lập thành một cấp số cộng, ta phải có tính chất: \(a + c = 2b\)

Điều này có nghĩa là tổng của số đầu \(a\) và số cuối \(c\) phải là một số chẵn (vì \(2b\) luôn chẵn).

Để tổng \((a + c)\) là số chẵn, thì \(a\) và \(c\) phải cùng tính chẵn lẻ (tức là cùng là số chẵn hoặc cùng là số lẻ).

Nhận xét quan trọng: Khi bạn chọn được 2 số đầu và cuối (\(a\) và \(c\)) có cùng tính chẵn lẻ, thì số ở giữa (\(b = \frac{{a + c}}{2}\)) sẽ là duy nhất và chắc chắn là số nguyên nằm giữa \(a\) và \(c\).

\( \Rightarrow \) Bài toán quy về việc: Chọn ngẫu nhiên 2 tấm thẻ từ tập hợp sao cho 2 tấm đó cùng chẵn hoặc cùng lẻ.

Tập hợp \(S = \{ 1,2,3,...,102\} \) có 102 phần tử.

Số lượng số lẻ là: \(\{ 1,3,5,...,101\} \). Số lượng = \(\frac{{101 - 1}}{2} + 1 = 51\) số.

Số lượng số chẵn là: \(\{ 2,4,6,...,102\} \). Số lượng = \(\frac{{102 - 2}}{2} + 1 = 51\) số.

Để có 3 số lập thành cấp số cộng, ta cần chọn 2 số đầu cuối \(a,c\) từ cùng một nhóm (chẵn hoặc lẻ):

+ Trường hợp 1: Chọn 2 số đều là số lẻ.

Số cách chọn 2 số từ 51 số lẻ là tổ hợp chập 2 của 51: \(C_{51}^2 = \frac{{51.50}}{2} = 1275{\rm{ (c\'a ch)}}\).

(Ví dụ: Chọn 1 và 5 thì số ở giữa chắc chắn là 3. Bộ là 1, 3, 5)

+ Trường hợp 2: Chọn 2 số đều là số chẵn.

Số cách chọn 2 số từ 51 số chẵn là tổ hợp chập 2 của 51: \(C_{51}^2 = \frac{{51.50}}{2} = 1275{\rm{ (c\'a ch)}}\).

(Ví dụ: Chọn 2 và 10 thì số ở giữa chắc chắn là 6. Bộ là 2, 6, 10)

Bước 3: Tổng hợp kết quả.

Tổng số cách lấy được ba tấm thẻ lập thành cấp số cộng là:

1275 + 1275 = 2550 cách