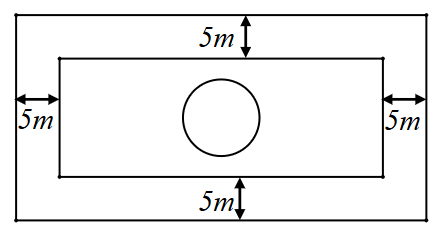
Trên mảnh đất có dạng hình chứ nhật với chiều rộng là \(x\) (m), chiều dài gấp đôi chiều rộng, người ta dự định làm một vườn hoa hình chữ nhật và bớt ra một phần đường đi rộng 5 m. Ở giữa vườn hoa, người ta làm một bể phun nước có hình tròn bán kính \(a\) (m). (Lấy \(\pi = 3,14\)).

Khi đó:

Cho hai biểu thức \(P\left( x \right) = {x^3} - 2ax + {a^2};\,\,Q\left( x \right) = {x^2} - \left( {3a + 1} \right)x + {a^2}\). Tìm giá trị \(a\) thỏa mãn sao cho \(P\left( 2 \right) = Q\left( 3 \right)\). (Kết quả ghi dưới dạng số thập phân)

Tìm giá trị của \(x\), biết: \(\left( {x - 2} \right)\left( {x + 3} \right) - x\left( {x - 2} \right) = 3\).

Tính giá trị của biểu thức \(B\left( x \right) = \left( {5{x^3} - 4{x^2}} \right):2{x^2} + \left( {3{x^4} + 6x} \right):3x - x\left( {{x^2} - 1} \right)\) tại \(x = 2.\)

Cho đa thức \(f\left( x \right) = {x^{100}} - 100{x^{99}} + 100{x^{98}} - ... + 100{x^2} - 100x + 2024\). Tính giá trị của \(f\left( x \right)\) tại \(x = 99\).

Cho đa thức \(A\left( x \right) = \left( {x - 3} \right)\left( {x + 3} \right) + \left( {x - 4} \right)\left( {x + 4} \right) - \left( {2{x^2} - 1} \right)\). Biết rằng thu gọn đa thức được\(A\left( x \right) = m\,\,\left( {m \in \mathbb{Z}} \right)\). Hỏi giá trị của \(m\) bằng bao nhiêu?

Cho hai đa thức \(A\left( x \right) = - 2{x^2} - {x^3} + 4{x^2} + {x^3} - 2 + 2x - 4 - x - {x^2}\) và \(B\left( x \right) = {x^2} - 2x + 2\). Biết \(A\left( x \right) - C\left( x \right) = B\left( x \right)\), khi đó:

Bậc của đa thức \(4{x^3} + {x^2} - 3x - 6\) là bậc mấy?