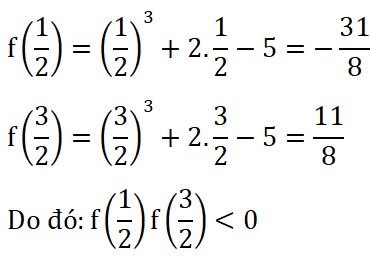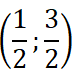Hãy tìm hai số a và b thỏa mãn , sao cho phương trình trong Ví dụ 3 ở trên có ít nhất một nghiệm thuộc khoảng .
Câu hỏi trong đề: Giải toán 11: Đại số và Giải tích !!
Quảng cáo
Trả lời:
Ta có:
y = f(x) là hàm số đa thức liên tục trên R.
Do đó f(x)liên tục trên
Từ đó suy ra, phương trình f(x) = 0 có ít nhất một nghiệm xo ∈ (0;2)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đặt f(x) = 2x3 – 6x + 1
TXĐ: D = R
f(x) là hàm đa thức nên liên tục trên R.
Ta có: f(-2) = 2.(-2)3 – 6(-2) + 1 = - 3 < 0
f(0) = 1 > 0
f(1) = 2.13 – 6.1 + 1 = -3 < 0.
⇒ f(-2).f(0) < 0 và f(0).f(1) < 0
⇒ f(x) = 0 có ít nhất một nghiệm thuộc khoảng (-2; 0) và ít nhất một nghiệm thuộc (0 ; 1)
⇒ phương trình f(x) = 0 có ít nhất hai nghiệm.
Lời giải
Xét hàm số g(x) = x – cos x liên tục trên R.
do đó liên tục trên đoạn [-π; π] ta có:
g(-π) = -π – cos (-π) = -π + 1 < 0
g(π) = π – cos π = π – (-1) = π + 1 > 0
⇒ g(-π). g(π) < 0
⇒ phương trình x – cos x = 0 có nghiệm trong (-π; π) tức là cos x = x có nghiệm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.