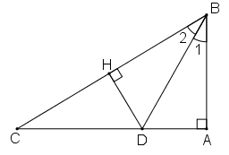
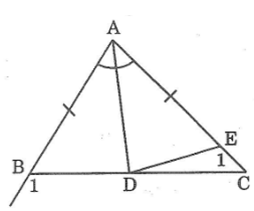
Cho tam giác ABC vuông tại A, tia phân giác của góc B cắt AC ở D. So sánh các độ dài AD, DC.
Câu hỏi trong đề: Sách bài tập Toán 7 Tập 2 !!
Quảng cáo
Trả lời:
Kẻ DH ⊥ BC.
Xét hai tam giác vuông ABD và HBD, ta có:
∠B1 = ∠B2 ( vì BD là tia phân giác của góc ABC).
Cạnh huyền BD chung
∠BAD = ∠BHD = 90º
Suy ra: ΔABD = ΔHBD (cạnh huyền, góc nhọn)
⇒ AD = HD (2 cạnh tương ứng) (1)
Trong tam giác vuông DHC có ∠DHC = 90o
⇒ DH < DC (cạnh góc vuông nhỏ hơn cạnh huyền) (2)
Từ (1) và (2) suy ra: AD < DC
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
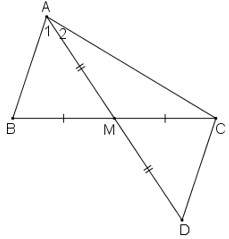
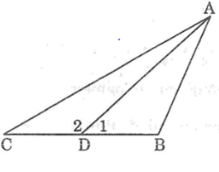
Trên tia đối tia MA lấy điểm D sao cho MD = MA
Xét ΔAMB và ΔDMC, ta có:
MA = MD (theo cách vẽ)
∠(AMB) = ∠(DMC) (đối đỉnh)
MB = MC (gt)
Suy ra: ΔAMB = ΔDMC (c.g.c)
Suy ra: AB = CD (2 cạnh tương ứng)
và ∠D = ∠A1(2 góc tương ứng) (1)
Mà AB < AC (gt)
nên: CD < AC
Trong ΔADC, ta có: CD < AC
Suy ra: ∠D > ∠A2(đối diện cạnh lớn hơn là góc lớn hơn) (2)
Từ (1) và (2) suy ra: ∠A1 > ∠A2hay ∠(BAM) > ∠(MAC) .
Lời giải
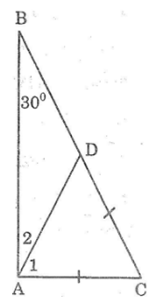
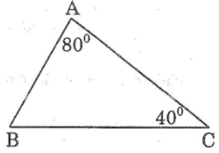
Xét ΔABC, ta có: ∠A= 90o; ∠B= 30o
Trên cạnh BC lấy điểm D sao cho CD = AC
Ta có: ΔACD cân tại C
Mà ∠C + ∠B = 90o (tính chất tam giác vuông)
Suy ra: ∠C = 90o - ∠B = 90o - 30o = 60o
Suy ra: ΔACD đều
Suy ra: AC = AD = DC và ∠A1= 60o
Ta có: ∠A1+ ∠A2 = ∠BAC = 90o
⇒ ∠A2 = 90o - ∠A1 = 90o - 60o = 30o
Trong ΔADB, ta có: ∠A2 = ∠B= 30o
Suy ra: ΔADB cân tại D (vì có 2 góc kề cạnh AB bằng nhau)
Hay AD = DB
Suy ra: AC = CD = DB mà CD + DB = BC
Vậy AC = 1/2 BC.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.