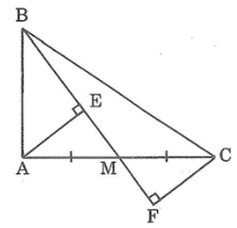
Cho tam giác ABC vuông tại A, M là trung điểm của AC. Gọi E và F là chân các đường vuông góc kẻ từ A và C đến đường thẳng BM. Chứng minh rằng AB < (BE + BF) / 2 .
Câu hỏi trong đề: Sách bài tập Toán 7 Tập 2 !!
Quảng cáo
Trả lời:
Trong ΔABM, ta có ∠(BAM) = 90o
Suy ra: AB < BM (trong tam giác vuông cạnh huyền lớn nhất)
Mà BM = BE + EM = BF - MF
Suy ra: AB < BE + EM
AB < BF - FM
Suy ra:AB + AB < BE + ME + BF - MF (1)
Xét hai tam giác vuông AEM và CFM, ta có:
∠(AEM) = ∠(CFM) = 90o
AM = CM (gt)
∠(AME) = ∠(CMF) (đối đỉnh)
Suy ra: ΔAEM = ΔCFM (cạnh huyền - góc nhọn)
Suy ra: ME = MF (2)
Từ (1) và (2) suy ra: AB + AB < BE + BF
Suy ra: 2AB < BE + BF
Vậy AB < (BE + BF) / 2 .
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
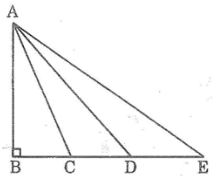
+ Ta có BC < BD < BE.
Mà AC, AD, AE là các đường xiên tương ứng với các hình chiếu BC, BD, BE
Suy ra AC < AD < AE.
+ AB là đường vuông góc nên AB nhỏ nhất trong tất cả các đường xiên và đường vuông góc.
Do đó AB < AC < AD < AE.
Lời giải
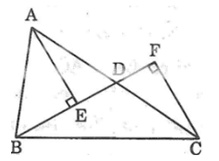
+ AE là đường vuông góc hạ từ đỉnh A xuống đường thẳng BF
⇒ AE < AD. ( quan hệ đường vuông góc và đường xiên). (1)
+ CF là đường vuông góc hạ từ đỉnh C xuống đường thẳng BF
⇒ CF < CD ( quan hệ đường vuông góc và đường xiên). (2)
Từ (1) và (2) vế cộng vế ta được: AE + CF < AD + CD = AC.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.