Bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
30 người thi tuần này 5.0 45.8 K lượt thi 17 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
20 câu Trắc nghiệm Toán 7 Cánh diều Ôn tập chương VI (Đúng sai - Trả lời ngắn) có đáp án
Danh sách câu hỏi:
Lời giải
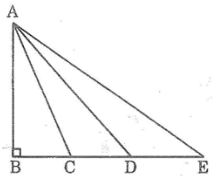
+ Ta có BC < BD < BE.
Mà AC, AD, AE là các đường xiên tương ứng với các hình chiếu BC, BD, BE
Suy ra AC < AD < AE.
+ AB là đường vuông góc nên AB nhỏ nhất trong tất cả các đường xiên và đường vuông góc.
Do đó AB < AC < AD < AE.
Lời giải
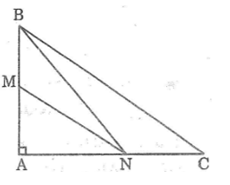
Nối BN.
+ Ta có: AM < AB
Mà NM, NB là các đường xiên ứng với hình chiếu AM, AB
⇒ NM < NB (1)
+ Lại có AN < AC.
Mà BN, BC là các đường xiên ứng với hình chiếu AN, AC
⇒ BN < BC (2)
Từ (1) và (2) suy ra: MN < BC
Lời giải
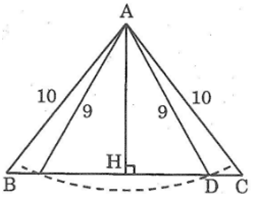
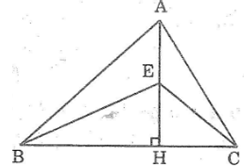
Kẻ AH ⊥ AB.
Xét hai tam giác vuông AHB và AHC, ta có:
∠AHB = ∠AHC = 90o
AB = AC (gt)
AH cạnh chung
Suy ra: ΔAHB = ΔAHC
(cạnh huyền - cạnh góc vuông)
Suy ra: HB = HC (hai cạnh tương ứng)
Ta có: HB = HC = BC/2 = 6 (cm)
Trong tam giác vuông AHB có ∠AHB = 90o
Áp dụng định lí Pi-ta-go, ta có:
AB2 = AH2 + HB2 ⇒ AH2 = AB2 – HB2 = 102 – 62 = 64
⇒ AH = 8 (cm)
Do bán kính cung tròn 9(cm) > 8(cm) nên cung tròn tâm A bán kính 9 cm cắt đường thẳng BC.
Gọi D là giao điểm của cung tròn tâm A bán kính 9 cm với BC.
Vì đường xiên AD < AC nên hình chiếu HD < HC.
Do đó D nằm giữa H và C.
Vậy cung tròn tâm A bán kính 9 cm cắt cạnh BC.
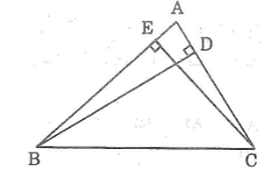
Lời giải
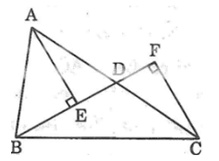
+ AE là đường vuông góc hạ từ đỉnh A xuống đường thẳng BF
⇒ AE < AD. ( quan hệ đường vuông góc và đường xiên). (1)
+ CF là đường vuông góc hạ từ đỉnh C xuống đường thẳng BF
⇒ CF < CD ( quan hệ đường vuông góc và đường xiên). (2)
Từ (1) và (2) vế cộng vế ta được: AE + CF < AD + CD = AC.
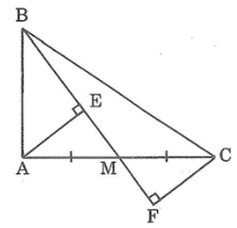
Lời giải
Trong ΔABM, ta có ∠(BAM) = 90o
Suy ra: AB < BM (trong tam giác vuông cạnh huyền lớn nhất)
Mà BM = BE + EM = BF - MF
Suy ra: AB < BE + EM
AB < BF - FM
Suy ra:AB + AB < BE + ME + BF - MF (1)
Xét hai tam giác vuông AEM và CFM, ta có:
∠(AEM) = ∠(CFM) = 90o
AM = CM (gt)
∠(AME) = ∠(CMF) (đối đỉnh)
Suy ra: ΔAEM = ΔCFM (cạnh huyền - góc nhọn)
Suy ra: ME = MF (2)
Từ (1) và (2) suy ra: AB + AB < BE + BF
Suy ra: 2AB < BE + BF
Vậy AB < (BE + BF) / 2 .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.