Câu hỏi:
19/04/2020 1,484Hai tam giác ABC, A'B'C' vuông tại A và A' có AB = A'B', BC > B'C'.
Không sử dụng định lý Pytago, chứng minh rằng AC > A'C'
Câu hỏi trong đề: Sách bài tập Toán 7 Tập 2 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Dùng phản chứng:
- Giả sử AC < A'C'. Khi đó theo chứng minh câu a) ta có BC < B'C'. Điều này không đúng với giả thiết BC > B'C'.
Giả sử AC = A'C'. Khi đó ta có ΔABC = ΔA'B'C' (c.g.c). Suy ra BC = B'C'.
Điều này cũng không đúng với giả thiết BC > B'C'. Vậy ta phải có AC > A'C'.
(Nếu sử dụng định lý Pytago thì có thể giải bài toán sau)
Trong tam giác vuông ABC có BC 2= AB 2+ AC 2 (1)
Trong tam giác vuông A'B'C' có B'C' 2= A'B' 2+ A'C' 2 (2)
Theo giả thiết AB = A'B' nên từ (1) và (2) ta có:
- Nếu AC > A'C' thì AC 2 > A'C' 2, suy ra BC 2 > B'C' 2 hay BC > B'C'
- Nếu BC > B'C' thì BC 2 > B'C' 2, suy ra AC 2 > A'C' 2 hay AC > A'C'.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
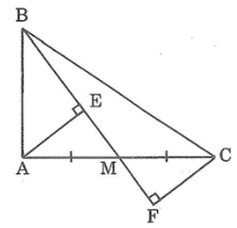
Trong ΔABM, ta có ∠(BAM) = 90o
Suy ra: AB < BM (trong tam giác vuông cạnh huyền lớn nhất)
Mà BM = BE + EM = BF - MF
Suy ra: AB < BE + EM
AB < BF - FM
Suy ra:AB + AB < BE + ME + BF - MF (1)
Xét hai tam giác vuông AEM và CFM, ta có:
∠(AEM) = ∠(CFM) = 90o
AM = CM (gt)
∠(AME) = ∠(CMF) (đối đỉnh)
Suy ra: ΔAEM = ΔCFM (cạnh huyền - góc nhọn)
Suy ra: ME = MF (2)
Từ (1) và (2) suy ra: AB + AB < BE + BF
Suy ra: 2AB < BE + BF
Vậy AB < (BE + BF) / 2 .
Lời giải
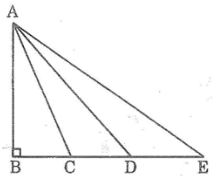
+ Ta có BC < BD < BE.
Mà AC, AD, AE là các đường xiên tương ứng với các hình chiếu BC, BD, BE
Suy ra AC < AD < AE.
+ AB là đường vuông góc nên AB nhỏ nhất trong tất cả các đường xiên và đường vuông góc.
Do đó AB < AC < AD < AE.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 02
-
15 câu Trắc nghiệm Toán 7 Cánh diều Bài 1: Tập hợp Q các số hữu tỉ có đáp án
-
Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 2