Bài 4: Tính chất ba đường trung tuyến của tam giác
34 người thi tuần này 5.0 45.8 K lượt thi 22 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
20 câu Trắc nghiệm Toán 7 Cánh diều Ôn tập chương VI (Đúng sai - Trả lời ngắn) có đáp án
Danh sách câu hỏi:
Lời giải
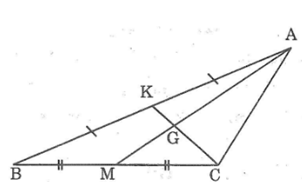
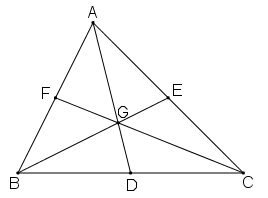
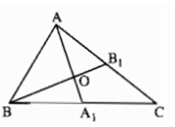
Theo hình vẽ ta có: AM và CK là hai đường trung tuyến của tam giác ABC. Hai đường trung tuyến này cắt nhau tại G nên G là trọng tâm tam giác ABC.
Áp dụng tính chất trọng tâm tam giác ta có:
GK = 1/3 CK; AG = 2GM; GK = 1/2 CG; AM = 3/2 AG; AM = 3GM
Lời giải
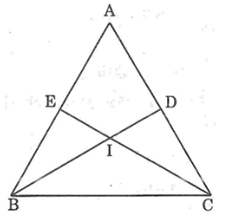
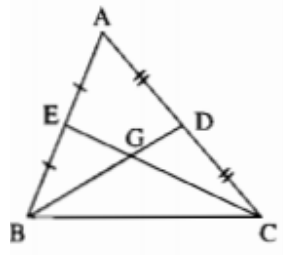
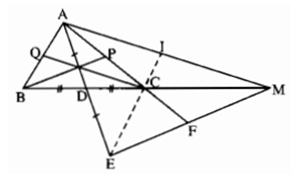
Giả sử ΔABC có hai đường trung tuyến BD và CE bằng nhau.
Gọi I là giao điểm BD và CE, ta có:
BI = 2/3 BD (tính chất đường trung tuyến) (1)
CI = 2/3 CE (tính chất đường trung tuyến) (2)
Từ (1), (2) và giả thiết BD = CE suy ra: BI = CI
Do BD = CE suy ra: BI + ID = CI + IE
Mà BI = CI ( chứng minh trên) nên : ID = IE
Xét ΔBIE và ΔCID, ta có:
BI = CI (chứng minh trên)
∠(BIE) = ∠(CID) (đối đỉnh)
IE = ID (chứng minh trên)
Suy ra: ΔBIE = ΔCID (c.g.c)
Suy ra: BE = CD (hai cạnh tương ứng) (3)
Lại có: BE = 1/2 AB (vì E là trung điểm AB) (4)
CD = 1/2 AC (vì D trung điểm AC) (5)
Từ (3), (4) và (5) suy ra: AB = AC.
Vậy tam giác ABC cân tại A.
Lời giải
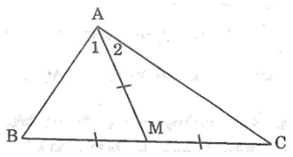
Xét ΔAMB và ΔAMC, ta có:
AB = AC (gt)
BM = CM (vì M là trung điểm BC)
AM cạnh chung
Suy ra: ΔAMB = ΔAMC (c.c.c)
Suy ra: ∠(AMB) = ∠(AMC) (1)
Lại có: ∠(AMB) + ∠(AMC) = 180o (hai góc kề bù) (2)
Từ (1) và (2) suy ra: ∠(AMB) = ∠(AMC) = 90o
Vậy AM ⊥ BC.
Lời giải
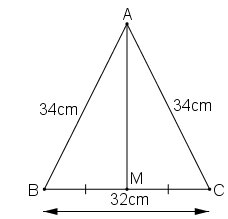
Do M là trung điểm của BC nên BM = CM = BC/2 cm
Tam giác AMB có ∠(AMB) = 90o
Áp dụng định lí Pi-ta-go vào tam giác vuông AMB, ta có:
AB2 = AM2 + BM2 ⇒ AM2 = AB2 - BM2 = 342 - 162
= 1156 - 256 = 900
Suy ra: AM = 30 (cm).
Lời giải
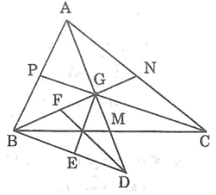
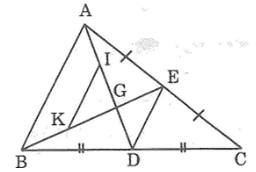
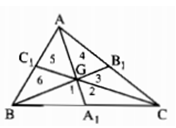
Gọi AM, BN, CP lần lượt là các đường trung tuyến của ΔABC. Các đường trung tuyến cắt nhau tại G.
Ta có: AG = GD (gt)
AG = 2GM (tính chất đường trung tuyến)
Suy ra: GD = 2GM
Mà GD = GM + MD ⇒ GM = MD
Xét ΔBMD và ΔCMG, ta có:
BM = CM (gt)
∠(BMD) = ∠(CMG) (đối đỉnh)
MD = GM (chứng minh trên)
Suy ra: ΔBMD = ΔCMG (c.g.c)
⇒ BD = CG (hai cạnh tương ứng)
Mặt khác: CG = 2/3 CP (tính chất đường trung tuyến)
Suy ra: BD = 2/3 CP (1)
Lại có: BG = 2/3 BN (tính chất đường trung tuyến) (2)
Và AG = 2/3 AM (tính chất đường trung tuyến)
Suy ra: GD = 2/3 AM (3)
Từ (1), (2) và (3) suy ra các cạnh của tam giác BGD bằng 2/3 các đường trung tuyến của tam giác ABC.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.