Ôn tập chương 3 - Phần Hình học
36 người thi tuần này 5.0 45.8 K lượt thi 33 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
20 câu Trắc nghiệm Toán 7 Cánh diều Ôn tập chương VI (Đúng sai - Trả lời ngắn) có đáp án
Danh sách câu hỏi:
Lời giải
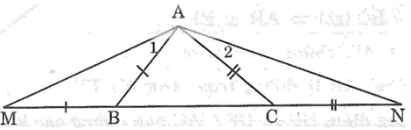
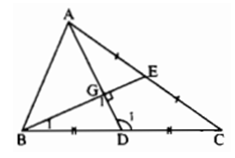
Trong ΔABC, ta có AC > AB
Suy ra: ∠(ABC) > ∠(ACB) (đối diện với cạnh lớn hơn là góc lớn hơn) (1)
Ta có: AB = BM (gt) ⇒ ΔABM cân tại B
Suy ra: ∠(AMB) = ∠A1(tính chất tam giác cân)
Trong ΔABM, ta có ∠(ABC) là góc ngoài tại đỉnh B
Suy ra: ∠(ABC) = ∠(AMB) + ∠A1 hay : ∠(ABC) = 2.∠(AMB)
Suy ra: ∠(AMB) = 1/2 ∠(ABC) (2)
Lại có: AC = CN (gt) ⇒ ΔACN cân tại C
Suy ra: ∠(ANC) = ∠A2(tính chất tam giác cân)
Trong ΔACN, ta có ∠(ACB) là góc ngoài tại đỉnh C
Suy ra: ∠(ACB) = ∠(ANC) + ∠A2 hay ∠(ACB) = 2∠(ANC)
Suy ra: ∠(ANC) = 1/2 ∠(ACB) (3)
Từ (1), (2) và (3) suy ra: ∠(AMB) > ∠(ANC) .
Lời giải
Trong ΔAMN, ta có: ∠(AMB) > ∠(ANC)
Suy ra: AN > AM (đối diện với góc lớn hơn là cạnh lớn hơn).
Lời giải
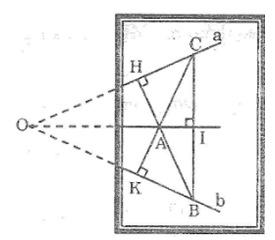
Ta có: AB < AC (gt)
Suy ra: HB < HC (đường xiên lớn hơn thì hình chiếu lớn hơn)
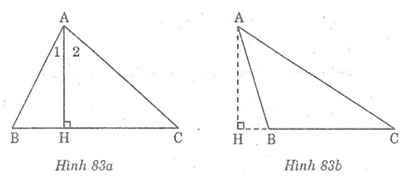
* Trường hợp Bnhọn (hình 83a)
Trong Δ ABC, ta có: AB < AC
Suy ra: ∠B > ∠C(đối diện với cạnh lớn hơn là góc lớn hơn)
Trong Δ AHB, ta có ∠(AHB) = 90o
Suy ra: ∠B + ∠(HAB) = 90o (tính chất tam giác vuông) (1)
Trong Δ AHC, ta có ∠(AHC) = 90o
Suy ra: ∠C + ∠(HAC) = 90o (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: ∠B + ∠(HAB) = ∠C + ∠(HAC)
Mà ∠B > ∠C nên ∠(HAB) < ∠(HAC)
* Trường hợp Btù (hình 83b)
Vì điểm B nằm giữa H và C nên ∠(HAC) = ∠(HAB) + ∠(BAC)
Vậy ∠(HAB) < ∠(HAC).
Lời giải
Ta có: 1 = 3 - 2 = 4 - 3 = 5 - 4
Suy ra: trong 3 cạnh của tam giác không có cạnh nào có độ dài 1cm.
* Nếu cạnh nhỏ nhất là 2cm
Ta có: 4 - 3 < 2 < 4 + 3; 5 - 4 < 2 < 5 + 4
Suy ra: hai cạnh kia là 3cm và 4cm hoặc 4cm và 5cm
* Nếu cạnh nhỏ nhất là 3cm
Ta có: 5 - 4 < 3 < 5 + 4; 3 = 5 - 2; 3 > 4 - 2
Như vậy hai cạnh kia là 5cm và 4cm
* Không có trường hợp cạnh nhỏ nhất là 4cm
Vậy có thể vẽ được ba tam giác với độ dài các cạnh là:
2cm; 3cm; 4cm
2cm; 4cm; 5cm
3cm; 4cm; 5cm
Lời giải
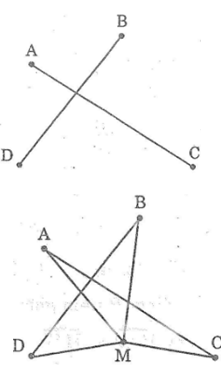
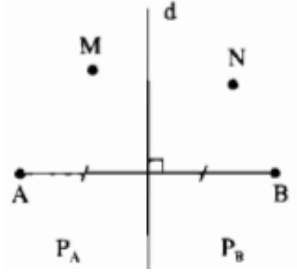
* Nếu M không trùng với giao điểm của AC và BD
Trong ΔAMC, ta có: MA + MC > AC (bất đẳng thức tam giác)
Trong ΔMBD, ta có: MB + MD > BD (bất đẳng thức tam giác)
* Nếu M trùng với giao điểm AC và BD
Ta có: MA + MC = AC
MB + MD = BD
+) Kết hợp cả hai trường hợp, suy ra: MA + MC ≥ AC
Và MB + MD ≥ BD (dấu bằng xảy ra khi M trùng với giao điểm của AC và BD)
Suy ra: MA + MB + MC + MD ≥ AC + BD
Vậy MA + MB + MC + MD = AC + BD bé nhất khi đó M là giao điểm của AC và BD.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.